计算机图形学中的颜色、光照与变换
本文详细介绍计算机图形学中的颜色视觉原理、光照模型与几何变换基础,探讨从人眼感知机制到颜色空间表示,以及Phong光照模型的数学原理与实现方法。
计算机图形学是一个迷人且应用广泛的领域,它研究如何在计算机中表示、创建和操纵视觉内容。从电影特效、视频游戏到科学可视化和工业设计,图形学技术无处不在。本文旨在介绍计算机图形学中的一些基础且重要的概念,为后续深入学习奠定基础。内容主要涵盖了颜色视觉、图像表示、三维模型、光照与着色以及几何变换等核心主题。
图形学中的一些重要概念
本篇博文将依次探讨以下几个图形学的基础概念:
- 颜色视觉 (Color Vision):理解光与人眼如何感知颜色。
- 图像和像素 (Images and Pixels):数字图像的基本构成。
- 三角网格模型 (Triangle Mesh Models):表示三维物体形状的常用方法。
- Phong光照模型与明暗处理 (Phong Lighting Model and Shading):模拟光照,赋予物体真实感。
- 视点变换和视点方向 (View Transformation and Direction):在三维空间中观察和定位物体。
颜色视觉
什么是颜色?
颜色本质上是人眼对不同波长的光的能量的感知。我们所说的“光”是电磁波 (electromagnetic waves) 的一种形式。不同波长的电磁波对应着不同的颜色感知。人眼能够感知到的光被称为可见光,其波长范围大约在 380 纳米 (nm) 到 760 纳米之间。
光的谱分布
通常我们遇到的“光”并非单一波长,而是由不同波长的电磁波按照某种能量分布混合叠加而成。例如,我们常说的“白光”通常被认为是由所有可见波长的电磁波以大致相等的强度混合得到的。描述光在各个可见波长分量的强度分布函数被称为光的谱分布 (Spectral Power Distribution, SPD)。
与光类似,物体呈现的颜色也可以使用谱分布函数来进行描述。人眼最终感知到的颜色由三个主要因素决定:
- 照明条件 (Illumination):光源发出的光的谱分布。
- 物体材质 (Material):物体的反射光谱特性,即它对各个波长光的吸收和反射能力。这通常由双向反射分布函数 (Bidirectional Reflectance Distribution Function, BRDF) 来描述(将在后续内容中详细介绍)。
- 观察条件 (Observer):光线进入人眼后,对视网膜上视觉感受器产生的刺激。
异谱同色 (Metamerism)
一个有趣的现象是,即使光的物理谱分布不同,人眼也可能感知到相同的颜色。
- 照明变化下的同色感知:如果控制观察条件和物体材质不变,在不同的照明条件下,物体仍可能被感知为相同的颜色。例如,一个只反射红光的物体,无论是在白光下还是在红光下照射,看起来都是红色的。
- 异谱同色现象:在观察条件不变的情况下,不同的物体材质(具有不同的反射光谱)在某种特定的照明条件下,也可能被感知为同一种颜色。一个经典的例子是,紫色光(波长约 400-450nm)的颜色感知,可以通过混合红光(约 620-750nm)和蓝光(约 450-495nm)来实现,尽管它们的物理光谱完全不同。
认识我们的眼睛
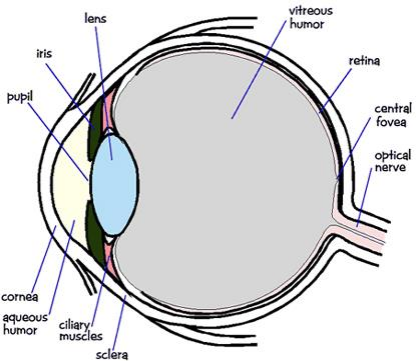
要理解颜色视觉,我们需要了解人眼的结构。光线首先通过角膜 (Cornea),然后穿过瞳孔 (Pupil)(由虹膜 (Iris) 控制大小),再经过晶状体 (Lens) 聚焦,穿过玻璃体 (Vitreous Humor),最终投射到眼球后部的视网膜 (Retina) 上。视网膜上的感光细胞将光信号转化为神经信号,通过视神经 (Optic Nerve) 传递给大脑。中央凹 (Fovea) 是视网膜上视觉最敏锐的区域。
视网膜——我们的感知器!
视网膜是实现光电转换的关键部位,包含多种细胞:
- 杆状细胞 (Rods):数量庞大(约1.2亿个),对亮度(光强)非常敏感,但在区分颜色方面能力较弱。它们是我们在夜间或弱光条件下视力的主要贡献者。
- 锥状细胞 (Cones):数量相对较少(约500-600万个),负责感知色彩。根据其对不同波长光的敏感度峰值,主要分为三类:对红光敏感(L-cones)、对绿光敏感(M-cones)和对蓝光敏感(S-cones)。
- 神经节细胞 (Ganglion Cells):负责收集来自杆状细胞和锥状细胞的信号,并将其传递给视神经。
杆状细胞与锥状细胞的密度分布
感光细胞在视网膜上的分布并非均匀。锥状细胞高度集中在中央凹区域,这也是为什么我们在视野中心处的辨色能力最强。而杆状细胞则主要分布在视网膜的周边区域。
颜色空间 (Color Space)
为了能够以数学和系统化的方式描述、分类、存储和重现颜色,人们定义了各种颜色空间。常用的颜色空间包括:
- RGB (Red, Green, Blue):主要用于电子显示设备(如显示器、电视),是一种加色系统。
- CMY (Cyan, Magenta, Yellow):主要用于印刷行业,是一种减色系统。常与其变种 CMYK (加上 Key/Black 黑色) 一起使用。
- HSV (Hue, Saturation, Value) / HSB (Hue, Saturation, Brightness):更符合人类对颜色的直观感知(色调、鲜艳程度、明暗),便于艺术家进行颜色选择和调整。
- CIE XYZ:由国际照明委员会 (CIE) 定义,旨在包含所有人类可感知的颜色,常用于科学研究和颜色标准化。
为何采用 RGB 颜色空间?
RGB 颜色空间在计算机图形学中得到最广泛应用,其基础是人类视觉的三刺激理论 (Trichromatic Theory)。该理论指出,人眼视网膜中的三种锥状细胞分别对红、绿、蓝三种波长的光最为敏感。因此,通过混合这三种基色光,可以模拟出人眼感知到的大部分颜色。
RGB 颜色空间详解
在 RGB 颜色空间中,一种颜色通常通过一个三维向量 (r, g, b) 来表示,代表红、绿、蓝三个分量的强度。许多图形学中的颜色操作可以简化为对这三个通道分别进行独立处理。在计算机中,r, g, b 分量通常被规范化到 [0, 1] 范围内的浮点数,或者表示为 [0, 255] 范围内的 8 位无符号整数。
颜色可以表示为红 (R)、绿 (G)、蓝 (B) 三种基本颜色的线性组合: C = rR + gG + bB
RGB 颜色空间的图示: 通常将 RGB 空间想象为一个立方体,三个轴分别代表 R、G、B 分量,(0,0,0) 代表黑色,(1,1,1) 代表白色(假设分量在 [0,1] 范围内)。
RGB 的局限性: 一个重要的限制是,并非所有可见光颜色都能表示为 R, G, B 光波的正线性组合。这意味着 RGB 色域(Gamut)无法覆盖人眼能感知到的所有颜色。下图展示了所有可见光谱颜色对应的 RGB 分量值,可以看出某些波长需要负的 R 分量才能匹配。
CMY(K) 颜色空间
CMY 颜色空间采用青 (Cyan)、品红 (Magenta)、黄 (Yellow) 作为基本颜色,它们分别是红 (R)、绿 (G)、蓝 (B) 的补色 (complements)。
- 减色系统 (Subtractive Color System):与 RGB(加色系统)相对,CMY 是减色系统。在 CMY 中,(0,0,0) 代表白色(纸张的颜色),(1,1,1) 理论上代表黑色(所有光都被吸收)。
- 印刷应用:印刷品本身不发光,其颜色是通过油墨吸收特定波长的光并反射剩余光来呈现的。因此,印刷业使用减色模型。
- CMYK:仅使用 CMY 三种油墨混合得到的“黑色”通常不够深,偏向深灰色。为了得到纯正的黑色并扩大颜色表示范围(色域),印刷中通常会额外加入黑色 (K - Key) 油墨,形成 CMYK 系统。
RGB (加色) vs CMY (减色)
- 加性混合 (Additive Mixing):适用于主动发光的物体,如显示器。混合的光越多,颜色越亮,R+G+B = 白色。
- 减性混合 (Subtractive Mixing):适用于被动反射光的物体,如印刷品。混合的颜料越多,吸收的光越多,颜色越暗,C+M+Y = 理论黑色。
HSV 颜色空间
在一个 8 位的 RGB 颜色空间中,可以表示多达 $256 \times 256 \times 256 = 16,777,216$ 种颜色。然而,RGB 表示法不够直观。我们很难直接通过调整 R, G, B 值来实现“让颜色更鲜艳”或“让颜色更亮”这样的操作。
HSV 颜色空间提供了一种更直观的方式来选择和描述颜色,它包含三个分量:
- Hue (H, 色调/色相):描述颜色的基本属性,即我们通常说的红、橙、黄、绿、青、蓝、紫等。它通常表示为圆周上的角度 (0-360°)。
- Saturation (S, 饱和度/纯度):表示颜色的鲜艳程度。饱和度越高,颜色越纯;饱和度越低,颜色越接近灰色或白色。通常表示为 [0, 1] 或 [0%, 100%]。
- Value (V, 亮度/明度) / Brightness (B):表示颜色的明暗程度。亮度越高,颜色越亮;亮度越低,颜色越接近黑色。通常表示为 [0, 1] 或 [0%, 100%]。
HSV 空间通常被可视化为一个圆锥体或圆柱体。由于其直观性,HSV 在艺术设计领域、图像处理软件(如调色板)以及某些可视化应用(如分形图像着色)中非常受欢迎。它能更好地反映人眼对颜色差异的感知距离。
CIE XYZ 颜色空间
CIE XYZ 颜色空间由国际照明委员会 (Commission Internationale de l’Éclairage, CIE) 于 1931 年提出,是一个基于人类颜色感知实验数据建立的标准化颜色空间。
- 覆盖所有可感知颜色:与 RGB 不同,CIE XYZ 色彩空间的设计目标是能够表示人眼可以感知的所有颜色。其基色 X, Y, Z 是虚拟的,不能直接由物理光源产生,它们是通过对 RGB 基色进行线性变换得到的。
- 科学应用:由于其精确性和完整性,CIE XYZ 主要应用于颜色科学研究、工业颜色测量和色彩管理等领域。Y 分量被特别设计用来匹配人眼的亮度感知。
CIE XYZ 色度图 (Chromaticity Diagram): 为了在二维平面上可视化 CIE XYZ 色彩空间(不考虑亮度),通常使用色度坐标 x 和 y,定义为: $x = \frac{X}{X+Y+Z}$ $y = \frac{Y}{X+Y+Z}$ 绘制出的马蹄形区域即为 CIE 1931 色度图,它展示了所有可见颜色的色调和饱和度。光谱色(单色光)位于马蹄形边界上。
小练习:
单选题 (1分)
比较直观,适合于艺术领域的颜色模型是哪种?
A. RGB模型
B. XYZ模型
C. HSV模型
D. CMY模型
答案:C
图像和像素
图像的定义
在数字世界中,一张图像 (Image) 可以被看作是一个二维离散函数:$f(x, y)$。
- 定义域:函数 $f$ 的定义域是一个以矩阵形式排列的网格。网格中的每一个小单元被称为像素 (Pixel),是 “Picture Element” 的缩写。
- 分辨率 (Resolution):图像中像素的总数量,通常表示为
宽度 × 高度(例如,1600×1280)。 - 值域:函数 $f$ 在每个像素
(x, y)处的值代表该像素的颜色。这个值可以属于不同的色彩空间:- 一维:例如,灰度图,每个像素只有一个亮度值。
- 三维:例如,RGB 彩色图,每个像素有 R, G, B 三个分量。
- 四维:例如,RGBA 图,在 RGB 基础上增加了一个 Alpha (A) 通道,表示透明度(Opacity)。
- 更高维度:用于存储更复杂的信息,如多光谱图像。
三角网格模型
图形学的基本目标与三维表示
计算机图形学的一个核心目标是从虚拟的三维场景和特定的相机(视点)参数出发,生成二维图像。那么,这些三维场景是如何在计算机中表示的呢?
对于简单的几何体,如球体、长方体,可以直接用它们的几何方程来描述。然而,对于复杂的模型(如人、动物、复杂机械),通常需要更通用的表示方法。常见的有参数曲线和曲面,以及网格 (Mesh) 模型。
在各种网格模型中,三角网格 (Triangle Mesh) 因其简单性、灵活性以及易于硬件加速等优点,在计算机图形学中得到了最为广泛的应用。
三角网格的定义
一个三角网格由以下两部分组成:
- 顶点集合 (Vertices): $V = {v_1, v_2, \dots, v_n}$,其中每个 $v_i$ 是欧氏空间中的一个三维点坐标 $(x_i, y_i, z_i)$。
- 面片集合 (Faces / Polygons): $F = {f_1, f_2, \dots, f_m}$,其中每个面片 $f_j$ 是一个由顶点集合 $V$ 中的三个顶点构成的空间三角形。例如, $f_1 = (v_{a1}, v_{b1}, v_{c1})$,其中 $v_{a1}, v_{b1}, v_{c1} \in V$。
示例: 上面提到的模型“牛”展示了三角网格的线框结构。模型“龙”和“人头”则是利用三角网格进行绘制并应用了着色 (Shading) 的结果(例如,平滑着色 Smooth Shading 模式)。着色的概念将在后面详细介绍。
法向量 (Normals)
法向量是定义表面朝向和进行光照计算的关键信息。
- 面法向量 (Face Normal):对于一个三角面片,其法向量 $\mathbf{N}_f$ 是一个垂直于该面片所在平面的非零向量。通常可以通过构成三角形的两条边的叉乘来计算(例如,$\mathbf{N}_f = (v_b - v_a) \times (v_c - v_a)$)。
- 朝向:每个面片法向量有两个可能的朝向(方向相反)。法向量的朝向约定了三角面片的正面 (Front Face) 和反面 (Back Face)。通常使用右手定则:如果顶点按 $v_a, v_b, v_c$ 逆时针顺序排列时,法向量指向观察者,则该面为正面。
- 一致性:对于一个封闭的、连续可定向的三角网格整体,所有相邻的三角面片需要具有一致的法向量朝向(例如,都指向模型外部)。
- 顶点法向量 (Vertex Normal):为了实现平滑着色效果,通常需要为每个顶点定义一个法向量 $\mathbf{N}_v$。顶点法向量可以看作是该顶点处曲面的法线方向的近似。它通常通过对其周围(共享该顶点的)所有三角面片的法向量进行加权平均来计算。常见的计算方式有:
- 算术平均 (Arithmetic Mean):如果顶点 $v$ 被 $k$ 个面片 $f_1, \dots, f_k$ 共享,则 \(\mathbf{N}_v = \frac{\sum_{i=1}^{k} \mathbf{N}_{f_i}}{k}\) (计算后通常需要归一化)
- 按面积加权平均 (Area Weighted):赋予面积大的面片更大的权重。设 $S_{f_i}$ 为面片 $f_i$ 的面积。 \(\mathbf{N}_v = \frac{\sum_{i=1}^{k} S_{f_i} \mathbf{N}_{f_i}}{\sum_{i=1}^{k} S_{f_i}}\) (计算后通常需要归一化)
- 按角度加权平均 (Angle Weighted):赋予顶点 $v$ 在面片 $f_i$ 中所占的内角 $\theta_i$ 作为权重。 \(\mathbf{N}_v = \frac{\sum_{i=1}^{k} \theta_i \mathbf{N}_{f_i}}{\sum_{i=1}^{k} \theta_i}\) (计算后通常需要归一化)
三角网格的简单绘制
有了三角网格数据后,如何将其绘制到屏幕上呢?有两种基本方法:
- 基于颜色的绘制:
- 给三角网格的每个顶点指定一个颜色属性 (e.g., RGB 值)。
- 模型表面上任意一点的颜色,可以通过其所在三角面片的三个顶点颜色进行插值 (Interpolation) 得到(例如,重心坐标插值)。这种方式简单快速,但不涉及光照模拟。
- 基于光照的绘制:
- 为网格模型指定材质属性 (Material Properties),区分正面和反面的材质(如果需要)。
- 在场景中设定一个或多个虚拟的光源,构成光照环境 (Lighting Environment)。
- 根据光照模型 (Lighting Model) 来计算材质在不同光照条件下呈现出来的颜色。这能产生更具真实感的图像。
Phong 光照模型与明暗处理
为什么需要光照模型?
绘制一张图像的本质是计算屏幕上每个像素的颜色值(通常是 RGB)。仅仅使用物体本身的颜色(如基于顶点颜色的绘制)往往显得平淡、缺乏立体感。为了模拟真实世界中光线与物体表面的交互,我们需要使用光照模型 (Lighting Model)。
着色 (Shading) 就是利用光照模型来计算场景中物体表面上某点(着色点, Shading Point)对应到像素的颜色的过程。
执行着色计算的程序通常运行在图形处理器 (Graphics Processing Unit, GPU) 上,被称为着色器 (Shader)。现代图形 API(如 OpenGL、DirectX、Vulkan)都支持高度可编程的着色器,允许开发者自定义复杂的着色效果。
光照模型分类
光照模型用于计算从物体表面某点反射到观察者眼中的光线强度(进而得到颜色)。主要分为两类:
- 局部光照模型 (Local Illumination / Local Lighting):
- 只考虑从光源直接照射到物体表面的光线(直接光照, Direct Illumination)对该点颜色的影响。
- 计算相对简单快速,但忽略了光线在场景中物体间的多次反弹(如反射、折射)。
- Phong 模型就是一种经典的局部光照模型。
- 全局光照模型 (Global Illumination / Global Lighting):
- 除了直接光照,还考虑了光线在场景中其他物体表面发生反射、折射等作用后,间接照射到当前物体表面上的光线(间接光照, Indirect Illumination)。
- 计算通常非常复杂,需要光线追踪 (Ray Tracing)、辐射度 (Radiosity) 等技术。
- 能够模拟更丰富的现象,如软阴影、颜色渗透 (Color Bleeding)、焦散 (Caustics) 等,产生更强的真实感。
- 全局光照 = 直接光照 + 间接光照。
光照模型的历史简述
- 1967年, Wylie 等人: 首次在显示中加入光照效果,认为光强与距离成反比。
- 1970年, Bouknight: 提出了第一个较完整的反射模型,包含 Lambert 漫反射 和 环境光。
- 1971年, Gouraud: 提出了漫反射模型+颜色插值 的思想(Gouraud Shading)。
- 1975年, Bui Tuong Phong: 提出了图形学中影响深远的 Phong 光照模型,在漫反射和环境光基础上增加了高光 (Specular Highlight)。
- 之后: 上述模型多为经验模型 (Empirical Models),不完全符合物理规律,且未考虑阴影。
- 1986年, Jim Kajiya: 提出了渲染方程 (Rendering Equation),奠定了基于物理的渲染 (Physically-Based Rendering, PBR) 的理论基础。PBR 致力于更精确地模拟光的物理行为,是现代高质量渲染的主流方向(将在后续讨论辐射度量学和 BRDF)。
光的传播:反射与折射
理解光照模型需要了解光的基本传播定律:
- 反射定律 (Law of Reflection):
- 入射角等于反射角 ($\theta_i = \theta_r$)。
- 入射光线、反射光线以及反射点处的表面法向量位于同一个平面内。
- 折射定律 (Law of Refraction / Snell’s Law):当光从一种介质传播到另一种介质时(例如从空气到水),其路径会发生偏折。
- 入射角 $\theta_i$ 和折射角 $\theta_t$ 的正弦值之比是一个常数,该常数仅取决于两种介质的性质,称为相对折射率 ($n = n_2 / n_1$):$n_1 \sin \theta_i = n_2 \sin \theta_t$。
- 入射光线、折射光线以及界面法向量位于同一个平面内。
光的度量基本概念
为了定量描述光,需要引入一些度量单位:
- 立体角 (Solid Angle, $\omega$): 衡量从某个观察点 P 看一个物体时,该物体所张开的“视角”大小。单位是球面度 (steradian, sr)。一个点周围的总立体角为 $4\pi$ sr。定义为 $d\omega = \frac{dS}{r^2}$,其中 $dS$ 是距离 $r$ 处球面上的一小块面积。
- 光通量 (Luminous Flux, $F$): 单位时间内通过某个面元 $dS$ 的总光能量。单位是流明 (lumen, lm)。
- 发光强度 (Luminous Intensity, $I$): 光源在给定方向上单位立体角内发出的光通量。$I = \frac{dF}{dω}$。单位是坎德拉 (candela, cd),cd = lm/sr。
- 光亮度 (Radiance, $L$): 描述一束光线携带能量的物理量,定义为单位投影面积、单位立体角内的光通量。$L = \frac{dF}{d\omega dA \cos\theta}$,其中 $dA$ 是面元面积,$\theta$ 是法线与光线方向的夹角。单位是 $cd/m^2$ (或 $W/(sr \cdot m^2)$ 在辐射度量学中)。在图形学中,我们计算的就是到达视点的 Radiance。
Phong 光照模型详解
Phong 模型是一种广泛使用的局部光照模型,用于计算在给定光源和观察方向下,物体表面某点反射出的光亮度(近似)。它假设反射光由三个分量组成:环境光 (Ambient)、漫反射 (Diffuse) 和 镜面反射 (Specular)。
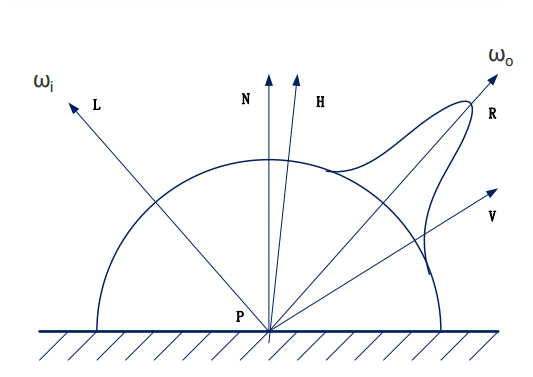
符号约定:
- $\mathbf{P}$: 着色点 (Shading Point)
- $\mathbf{N}$: 着色点 $\mathbf{P}$ 处的单位表面法向量 (Normal)
- $\boldsymbol{\omega}_i$: 从 $\mathbf{P}$ 指向光源的单位向量 (Incident light direction)
- $\boldsymbol{\omega}_o$ / $\mathbf{V}$: 从 $\mathbf{P}$ 指向视点 (Viewer/Camera) 的单位向量 (Outgoing view direction)
- $\mathbf{R}$: 入射光 $\boldsymbol{\omega}_i$ 关于法向量 $\mathbf{N}$ 的理想镜面反射方向 ($\mathbf{R} = 2(\mathbf{N} \cdot \boldsymbol{\omega}_i)\mathbf{N} - \boldsymbol{\omega}_i$)
- $\mathbf{H}$: 半程向量 (Halfway Vector),即 $\boldsymbol{\omega}_i$ 和 $\mathbf{V}$ 夹角的角平分线方向 ($\mathbf{H} = \frac{\boldsymbol{\omega}_i + \mathbf{V}}{||\boldsymbol{\omega}_i + \mathbf{V}||}$)。用于 Blinn-Phong 优化。
- $L_i(\boldsymbol{\omega}_i)$: 入射光携带的能量(亮度/Radiance)。
1. 漫反射光 (Diffuse Light): 模拟光线照射到粗糙表面后向各个方向均匀散射的现象。
- 特点: 反射强度与观察方向 $\mathbf{V}$ 无关(各向同性)。强度仅依赖于入射光线与表面法线的夹角。
- Lambert定律: 漫反射强度正比于入射光方向 $\boldsymbol{\omega}_i$ 与法向量 $\mathbf{N}$ 夹角的余弦值。
- 公式: \(L_d = k_d L_i(\boldsymbol{\omega}_i) \max(0, \mathbf{N} \cdot \boldsymbol{\omega}_i)\)
- $k_d$: 漫反射系数 (Diffuse Coefficient),是一个 RGB 向量 $(k_{dr}, k_{dg}, k_{db})$,表示物体表面对入射光能量的吸收和散射比例,通常与物体的固有颜色紧密相关。
- $\max(0, \mathbf{N} \cdot \boldsymbol{\omega}_i)$: 确保只有当光线从表面正面照射时才有贡献(点乘为正)。
2. 镜面反射光 (Specular Light) / 高光: 模拟光线照射到光滑表面(如金属、塑料)时产生的集中反射,形成高光区域。
- 特点: 反射强度与观察方向 $\mathbf{V}$ 密切相关,当 $\mathbf{V}$ 接近理想反射方向 $\mathbf{R}$ 时最强。
- 公式 (Phong): \(L_s = k_s L_i(\boldsymbol{\omega}_i) \max(0, \mathbf{R} \cdot \mathbf{V})^n\)
- 公式 (Blinn-Phong): 为了计算效率(避免计算 $\mathbf{R}$),常用半程向量 $\mathbf{H}$ 代替: \(L_s = k_s L_i(\boldsymbol{\omega}_i) \max(0, \mathbf{N} \cdot \mathbf{H})^n\)
- $k_s$: 镜面反射系数 (Specular Coefficient),通常是一个 RGB 向量,表示高光的颜色和强度,与物体表面的光滑程度有关。
- $n$: 反射指数 (Shininess exponent) 或 高光指数,是一个正数。$n$ 越大,表示表面越光滑,高光区域越小、越集中、越亮。
3. 环境光 (Ambient Light): 对全局光照中无法直接计算的间接光照(如来自环境的漫反射光)的一个简单近似。
- 特点: 假设场景中存在一个均匀的、来自所有方向的环境光。物体对环境光的反射也是均匀的,与 $\boldsymbol{\omega}_i$ 和 $\mathbf{V}$ 都无关。
- 公式: \(L_a = k_a I_a\)
- $k_a$: 环境光反射系数 (Ambient Coefficient),是一个 RGB 向量,表示物体对环境光的反射能力。
- $I_a$: 环境光强度 (Ambient Intensity),是一个 RGB 常量,代表场景中环境光的整体亮度和颜色。
- 局限性: 这是一个非常粗糙的近似,因为它假设间接光照在所有地方都是恒定且均匀的,这与现实不符。
总光照: 最终,Phong 模型计算出的从 $\mathbf{P}$ 点反射到视点 $\mathbf{V}$ 的总光亮度 $L$ 是这三个分量的和: \(L = L_a + L_d + L_s = k_a I_a + k_d L_i(\boldsymbol{\omega}_i) \max(0, \mathbf{N} \cdot \boldsymbol{\omega}_i) + k_s L_i(\boldsymbol{\omega}_i) \max(0, \mathbf{N} \cdot \mathbf{H})^n\) (这里使用了 Blinn-Phong 的镜面反射项)。
Phong 模型总结: Phong 模型虽然是经验模型,不完全符合物理规律(例如,不保证能量守恒),但它计算相对简单,并且能够产生视觉上可接受的包含漫反射和高光的图像效果,因此在实时渲染领域长期占据重要地位。
明暗处理 / 着色方法 (Shading Methods)
在将三维模型(通常是三角网格)渲染到二维图像时,我们需要确定如何为模型表面上的每个像素计算颜色。仅仅在模型顶点处计算光照是不够的,因为这会导致不平滑的外观。因此,需要结合光照模型和插值 (Interpolation) 技术来进行明暗处理 (Shading)。
常见的明暗处理方法有:
- 平面着色 (Flat Shading):
- 方法: 对每个三角面片只计算一次颜色(例如,使用面片中心点和面法向量进行光照计算),然后用这个单一颜色填充整个面片对应的像素。
- 效果: 结果呈现块状外观,能清晰看到每个三角面片。计算量最小。
- Gouraud 明暗处理 (Gouraud Shading):
- 提出者: Henri Gouraud (1971)。
- 方法:
- 首先,使用光照模型(如 Phong 模型)计算模型每个顶点的颜色。
- 对于三角面片内部的每个像素,其颜色通过对其所在面片三个顶点颜色进行重心坐标插值 (Barycentric Interpolation) 得到。
- 效果: 相较于 Flat Shading,能够产生平滑过渡的颜色,但通常无法正确表现高光(高光可能出现在面片内部,但 Gouraud 插值的是颜色,可能导致高光被平均掉或变形,尤其是在网格较稀疏时)。计算量适中。
- Phong 明暗处理 (Phong Shading):
- 提出者: Bui Tuong Phong (1973),注意与 Phong 光照模型区分。
- 方法:
- 首先,计算模型每个顶点的法向量(通常是平均顶点法向量)。
- 对于三角面片内部的每个像素,其法向量通过对其所在面片三个顶点法向量进行重心坐标插值得到。
- 在每个像素处,使用插值得到的法向量,应用光照模型(如 Phong 光照模型)来计算该像素的最终颜色。
- 效果: 能够产生非常平滑的着色效果,并且能更准确地表现高光,因为光照计算是在像素级别进行的。计算量相较于 Gouraud Shading 更大,但效果通常最好。现代 GPU 硬件采用的明暗处理方法基本都是 Phong Shading 或其变种。
小练习:
单选题 (1分)
Phong明暗处理能表示高光,是因为用了哪种插值?
A. 颜色插值
B. 重心坐标插值
C. 双线性插值
D. 法向插值
答案:D (虽然重心坐标插值是实现法向插值的机制,但关键在于插值的是法向量本身)
视点变换和视点方向
计算机图形学关注如何将由几何模型构成的三维场景绘制成高质量的二维图像。在这个过程中,变换 (Transformation) 扮演着至关重要的角色。通过变换,我们可以方便、高效地设置和编辑三维场景中的物体位置、大小、朝向,以及定义光源位置和观察者(相机/视点)的参数。
为什么需要变换?
假设我们有一个函数 drawUnitSquare() 可以绘制一个位于原点、边长为 1 的正方形 ([0,1] x [0,1])。现在需要绘制一个任意位置和大小、平行于坐标轴的矩形,其左下角坐标为 (lox, loy),右上角坐标为 (hix, hiy)。
一种方法:编写一个全新的函数
drawRect(lox, loy, hix, hiy),直接指定四个顶点的坐标。对于简单的矩形尚可,但如果需要绘制一个复杂模型(如茶壶)的多个实例,每个实例都有不同的位置、大小和朝向,为每个实例重新定义所有顶点坐标将极其繁琐和低效。利用变换的方法:我们可以重用
drawUnitSquare(),通过组合平移 (Translation) 和缩放 (Scaling) 变换来实现:1 2 3 4
// Pseudocode using OpenGL-like functions translate(lox, loy); // Move the origin to (lox, loy) scale(hix - lox, hiy - loy); // Scale the unit square to the desired size drawUnitSquare(); // Draw the transformed unit square
这种基于变换的解决方案更加快速、灵活和模块化。
在光栅化 (Rasterization) 渲染流程中,变换同样是核心环节。通过一系列变换(通常称为 MVP 变换),将三维模型的顶点坐标最终映射到二维屏幕上的像素坐标。
什么叫变换 (Transformation)?
从数学上讲,变换是一个函数,它将空间中的点 $\mathbf{x}$ 映射(改变)成另一个点 $\mathbf{x’}$。 $\mathbf{x’} = f(\mathbf{x})$
变换在图形学中有广泛应用,例如:
- 建模 (Modeling):定位、旋转、缩放物体。
- 动画 (Animation):改变物体随时间的位置、形状(变形 Morphing, 骨骼动画 Skinning)。
- 观察 (Viewing):设置相机的位置和朝向。
- 投影 (Projection):将三维场景投影到二维平面。
- 特效 (Effects):如实时阴影生成等。
变换的分类
常见的几何变换可以根据它们保持(或不改变)的几何属性进行分类:
- 刚体变换 (Rigid-body Transformation):
- 保持度量:长度、角度、面积、体积都不变。
- 包括:平移 (Translation)、旋转 (Rotation) 以及它们的任意组合。
- (注意:镜像/对称 (Reflection) 虽然保持长度,但改变了手性 (handedness),有时不被严格归为刚体变换,但属于等距变换 Isometry)。
- 相似变换 (Similarity Transformation):
- 保持角度和形状比例,但不一定保持长度或大小。
- 包括:刚体变换 + 均匀缩放 (Uniform Scaling)(所有方向缩放比例相同)及其组合。
- 线性变换 (Linear Transformation):
- 满足线性性质:$L(\mathbf{p}+\mathbf{q}) = L(\mathbf{p}) + L(\mathbf{q})$ 和 $L(a\mathbf{p}) = aL(\mathbf{p})$。
- 在几何上,线性变换保持原点不变(或将原点映射到原点),并将直线映射为直线。
- 包括:旋转 (Rotation)、缩放 (Scaling)(可以非均匀)、错切 (Shear)、对称 (Reflection)。
- 可以用矩阵乘法表示:$\mathbf{x’} = M \mathbf{x}$。
- 仿射变换 (Affine Transformation):
- 保持直线以及直线间的平行关系。两条平行的直线变换后仍然平行。
- 可以看作是线性变换与平移的组合。
- 包括:刚体变换、相似变换、线性变换、平移及其任意组合。
- 可以用矩阵乘法和平移向量相加表示:$\mathbf{x’} = M \mathbf{x} + \mathbf{t}$。
- 投影变换 (Projective Transformation) / 透视变换 (Perspective Transformation):
- 最一般的线性变换(在齐次坐标下),只保证直线变换后仍然是直线。平行关系、角度、长度通常都不保持。
- 用于实现相机的透视投影效果。
变换层级关系: (单位变换) ⊂ 刚体变换 ⊂ 相似变换 ⊂ 仿射变换 ⊂ 投影变换 (线性变换) ⊂ 仿射变换
变换的表示:矩阵与齐次坐标
考虑一个二维仿射变换: $x’ = ax + by + c$ $y’ = dx + ey + f$
可以写成矩阵形式: \(\begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} a & b \\ d & e \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} c \\ f \end{pmatrix}\) 或者简洁地写为 $\mathbf{p’} = M \mathbf{p} + \mathbf{t}$。这种表示方式不够统一,因为它包含了一个矩阵乘法和一个向量加法。这使得变换的组合(例如,先旋转再平移)表示起来比较复杂。
齐次坐标 (Homogeneous Coordinates): 为了用单一的矩阵乘法来表示所有仿射变换(甚至投影变换),我们引入齐次坐标。其核心思想是用 $d+1$ 维向量来表示 $d$ 维空间中的点和向量。
- 二维点 $(x, y)$ 在齐次坐标中表示为 $(x, y, 1)$。
- 三维点 $(x, y, z)$ 在齐次坐标中表示为 $(x, y, z, 1)$。
使用齐次坐标后,上述二维仿射变换可以统一表示为一个 3x3 矩阵与 3维齐次坐标向量的乘法: \(\begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{pmatrix} a & b & c \\ d & e & f \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}\) 即 $\mathbf{p’} = M \mathbf{p}$,其中 $\mathbf{p’}$ 和 $\mathbf{p}$ 是齐次坐标表示, $M$ 是 3x3 的仿射变换矩阵。
三维空间的齐次坐标: 在三维图形学中,我们使用 4 维齐次坐标 $(x, y, z, w)$ 和 4x4 的变换矩阵。 \(\begin{pmatrix} x' \\ y' \\ z' \\ w' \end{pmatrix} = \begin{pmatrix} a & b & c & d \\ e & f & g & h \\ i & j & k & l \\ m & n & o & p \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ w \end{pmatrix}\) 即 $\mathbf{p’} = M \mathbf{p}$。
- 点的表示: 通常,三维点 $(x, y, z)$ 表示为 $(x, y, z, 1)$ (即 $w=1$)。
- 向量的表示: 三维向量 $(x, y, z)$(表示方向和大小,与位置无关)表示为 $(x, y, z, 0)$ (即 $w=0$)。向量的这种表示使其在进行平移变换时保持不变,这符合向量的性质。
- 几何意义:
- 当 $w \neq 0$ 时,齐次坐标 $(x, y, z, w)$ 表示三维空间中的点 $(\frac{x}{w}, \frac{y}{w}, \frac{z}{w})$。这个从 $(x, y, z, w)$ 到 $(\frac{x}{w}, \frac{y}{w}, \frac{z}{w}, 1)$ 的过程称为透视除法 (Perspective Division) 或齐次坐标归一化。它在投影变换中非常重要。
- 当 $w = 0$ 时,齐次坐标 $(x, y, z, 0)$ 可以理解为沿着 $(x, y, z)$ 方向的无穷远点 (Point at Infinity),或者更直观地,表示一个方向向量。
基本仿射变换的 4x4 矩阵
使用齐次坐标,常见的仿射变换可以表示为 4x4 矩阵:
1. 平移 (Translation) by $(t_x, t_y, t_z)$: \(T(t_x, t_y, t_z) = \begin{pmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{pmatrix}\) 应用 $T$ 到点 $(x, y, z, 1)$ 得到 $(x+t_x, y+t_y, z+t_z, 1)$。 应用 $T$ 到向量 $(x, y, z, 0)$ 得到 $(x, y, z, 0)$(向量不受平移影响)。
2. 缩放 (Scaling) by $(s_x, s_y, s_z)$ relative to the origin: \(S(s_x, s_y, s_z) = \begin{pmatrix} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\) 如果 $s_x = s_y = s_z$,则为均匀缩放。
3. 旋转 (Rotation): 三维旋转有三个自由度。可以分解为绕三个主轴的旋转,或者表示为绕任意轴 $\mathbf{k}=(k_x, k_y, k_z)$ 旋转角度 $\theta$。
- 绕 Z 轴旋转 $\theta$: \(R_z(\theta) = \begin{pmatrix} \cos\theta & -\sin\theta & 0 & 0 \\ \sin\theta & \cos\theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\)
- 绕 X 轴旋转 $\theta$: \(R_x(\theta) = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta & 0 \\ 0 & \sin\theta & \cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\)
- 绕 Y 轴旋转 $\theta$: \(R_y(\theta) = \begin{pmatrix} \cos\theta & 0 & \sin\theta & 0 \\ 0 & 1 & 0 & 0 \\ -\sin\theta & 0 & \cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\)
- 绕任意单位向量轴 $\mathbf{k}=(k_x, k_y, k_z)$ 旋转 $\theta$ (Rodrigues’ Rotation Formula): 设 $c = \cos\theta$, $s = \sin\theta$, $v = 1 - c$。 \(R(\mathbf{k}, \theta) = \begin{pmatrix} k_x^2 v + c & k_x k_y v - k_z s & k_x k_z v + k_y s & 0 \\ k_y k_x v + k_z s & k_y^2 v + c & k_y k_z v - k_x s & 0 \\ k_z k_x v - k_y s & k_z k_y v + k_x s & k_z^2 v + c & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\)
变换的复合 (Composition)
多个变换可以连续作用于一个点或物体。例如,先对点 $\mathbf{p}$ 进行缩放变换 $S$,再进行平移变换 $T$。 $\mathbf{p’} = T(S \mathbf{p})$
由于矩阵乘法满足结合律,这等价于先将变换矩阵 $T$ 和 $S$ 相乘得到一个复合变换矩阵 $M = TS$,然后用 $M$ 作用于 $\mathbf{p}$: $\mathbf{p’} = (TS) \mathbf{p} = M \mathbf{p}$
重要:矩阵乘法不满足交换律! 即 $TS \neq ST$。变换的顺序非常重要。
- 先缩放再平移 (Scale then Translate):$M = TS$。物体先在原点处缩放,然后平移到目标位置。
- 先平移再缩放 (Translate then Scale):$M’ = ST$。物体先平移,然后以新的原点(即平移后的位置)为中心进行缩放(如果缩放矩阵是以原点为中心的)。这通常会导致不同的结果。
法向量的变换
当我们对物体进行几何变换(特别是仿射变换中的非均匀缩放和错切)时,物体表面的法向量不能直接使用与顶点相同的变换矩阵 $M$ 来变换。为什么?
考虑一个表面和它上面的一点 $\mathbf{p}$,该点处的切向量 $\mathbf{v}$ 和法向量 $\mathbf{n}$。切向量位于切平面内,法向量垂直于切平面。因此,$\mathbf{n}^T \mathbf{v} = 0$ (点乘为零)。
当对物体施加变换 $M$ 时,点 $\mathbf{p}$ 变为 $\mathbf{p’} = M\mathbf{p}$,切向量 $\mathbf{v}$ 变为 $\mathbf{v’} = M\mathbf{v}$(对于仿射变换,切向量可以通过 $M$ 的线性部分变换)。变换后的法向量 $\mathbf{n’}$ 必须仍然垂直于变换后的切向量 $\mathbf{v’}$,即 $(\mathbf{n’})^T \mathbf{v’} = 0$。
我们有 $\mathbf{v} = M^{-1} \mathbf{v’}$。代入原始垂直条件: $\mathbf{n}^T (M^{-1} \mathbf{v’}) = 0$ $(\mathbf{n}^T M^{-1}) \mathbf{v’} = 0$
比较 $(\mathbf{n’})^T \mathbf{v’} = 0$ 和 $(\mathbf{n}^T M^{-1}) \mathbf{v’} = 0$,我们发现变换后的法向量 $\mathbf{n’}$ 的转置应该是 $\mathbf{n}^T M^{-1}$。 因此,$(\mathbf{n’})^T = \mathbf{n}^T M^{-1}$。 两边同时转置,得到: $\mathbf{n’} = (M^{-1})^T \mathbf{n}$
结论:如果顶点坐标使用变换矩阵 $M$ 进行变换,那么表面法向量应该使用 $M$ 的 逆矩阵的转置 (Inverse Transpose),记作 $(M^{-1})^T$ 或 $M^{-T}$,来进行变换。
对于刚体变换和均匀缩放(即相似变换),$(M^{-1})^T$ 正好等于 $M$ 的一个标量倍数,此时可以直接用 $M$ 变换法向量(之后需要重新归一化)。但对于非均匀缩放和错切等更一般的仿射变换,必须使用逆转置矩阵。
光栅化渲染流水线中的变换 (MVP Transform)
在典型的实时渲染(如光栅化)流水线中,为了将三维模型的顶点坐标最终转换到二维屏幕像素坐标,需要经历一系列的坐标空间变换。最核心的是 MVP 变换,包括三个主要阶段:
- 模型变换 (Model Transform / World Transform):
- 目的: 将物体从其局部坐标空间 (Local Space / Model Space) 变换到世界坐标空间 (World Space)。
- 作用: 在共享的世界场景中定位、定向和缩放每个物体实例。
- 变换: 通常是平移、旋转和缩放的组合,得到一个模型矩阵 M。
- $\mathbf{p}_{world} = M_{model} \mathbf{p}_{local}$
- 视图变换 (View Transform):
- 目的: 将场景从世界坐标空间变换到相机坐标空间 (Camera Space / View Space / Eye Space)。
- 作用: 相当于将整个世界移动和旋转,使得相机位于原点,看向某个特定方向(例如,看向 Z 轴负方向或正方向,Y 轴指向上方)。这使得后续的投影变换更加方便。
- 变换: 本质上是一个刚体变换(平移+旋转),得到一个视图矩阵 V。
- $\mathbf{p}_{camera} = M_{view} \mathbf{p}_{world} = M_{view} M_{model} \mathbf{p}_{local}$
- 投影变换 (Projection Transform):
- 目的: 将相机坐标空间中的点变换到裁剪空间 (Clip Space)。
- 作用: 定义相机的可视范围(视锥 View Frustum),并将这个范围内的几何体映射到一个规范的立方体区域(通常是 [-1, 1] x [-1, 1] x [-1, 1],称为规范化设备坐标 NDC, Normalized Device Coordinates)。同时,为后续的深度测试和透视效果做准备。
- 变换: 使用投影矩阵 P。可以是透视投影 (Perspective Projection) 或正交投影 (Orthographic Projection)。
- $\mathbf{p}_{clip} = M_{projection} \mathbf{p}_{camera} = M_{projection} M_{view} M_{model} \mathbf{p}_{local}$
合并变换: 通常将模型、视图、投影三个矩阵预先乘在一起,得到一个模型-视图-投影 (MVP) 矩阵: $M_{MVP} = M_{projection} M_{view} M_{model}$ $\mathbf{p}_{clip} = M_{MVP} \mathbf{p}_{local}$
从裁剪空间到屏幕坐标:
- 透视除法: 裁剪空间坐标 $\mathbf{p}_{clip} = (x_{c}, y_{c}, z_{c}, w_{c})$ 通过除以其 $w_{c}$ 分量,得到 NDC 坐标: $\mathbf{p}_{NDC} = (x_{c}/w_{c}, y_{c}/w_{c}, z_{c}/w_{c})$。 $x_{ndc}, y_{ndc}, z_{ndc}$ 的范围通常在 [-1, 1] 内。
- 视口变换 (Viewport Transform): 将 NDC 坐标 $(x_{ndc}, y_{ndc})$ 映射到最终屏幕上的像素坐标 $(x_{screen}, y_{screen})$。 $z_{ndc}$ 通常用于深度缓冲 (Depth Buffer) 进行可见性判断。
坐标空间总结: Local Space $\xrightarrow{Model}$ World Space $\xrightarrow{View}$ Camera Space $\xrightarrow{Projection}$ Clip Space $\xrightarrow{Perspective Division}$ NDC Space $\xrightarrow{Viewport}$ Screen Space
投影变换详解
投影变换模拟了人眼或相机将三维世界感知为二维图像的过程。它定义了一个视锥 (View Frustum),即相机能够看到的空间区域,通常由近裁剪面 (Near Plane)、远裁剪面 (Far Plane) 以及四个侧面确定。投影变换的目标是将这个视锥内的所有点映射到规范化的立方体 (NDC) 中。
1. 正交投影 (Orthographic Projection):
- 特点: 模拟视点在无穷远处进行的投影。所有投影线相互平行(通常垂直于投影平面)。物体的大小不随距离改变,缺乏透视效果(没有“近大远小”)。
- 应用: 常用于工程制图 (CAD)、2D 游戏或需要精确尺寸表示的场景。
- 变换: 本质上是一个缩放和平移,将一个由
left, right, bottom, top, near, far定义的长方体观察区域映射到 NDC 立方体 ([-1, 1]^3)。不需要进行透视除法(变换后的 $w$ 坐标通常保持为 1)。
2. 透视投影 (Perspective Projection):
- 特点: 模拟视点在有限距离处进行的投影。所有投影线汇聚于视点。产生“近大远小”的透视效果,更符合人类视觉习惯。
- 应用: 广泛用于 3D 游戏、电影、虚拟现实等追求真实感的场景。
- 变换: 将一个由视场角 (Field of View, FOV)、宽高比 (Aspect Ratio)、近裁剪面距离 (Near) 和远裁剪面距离 (Far) 定义的金字塔形视锥(截头体)映射到 NDC 立方体。
- 关键: 变换矩阵会将相机空间中的 $z$ 坐标信息编码到裁剪空间的 $w$ 坐标中。例如,一个简化的透视投影矩阵(假设投影到 $z=n$ 平面)会将点 $(x, y, z)$ 映射到 $(x’, y’, z’, z)$ 或类似的包含 $z$ 的 $w$ 分量。经过透视除法后,得到的 NDC 坐标 $x_{ndc} = x’/z$, $y_{ndc} = y’/z$ 就体现了近大远小的效果。深度值 $z_{ndc}$ 也会被非线性地映射到 [-1, 1] (或 [0, 1]) 范围内,用于深度测试。
透视投影矩阵 (示例): 一个常用的透视投影矩阵(将视锥映射到 NDC [-1, 1]^3,假设相机看向 -Z 方向,右手坐标系)形式如下(具体形式可能因 API 和约定略有不同): 令 $n$=近平面距离, $f$=远平面距离, $t$=top (由FOV和n决定), $r$=right (由aspect和t决定)。 \(P = \begin{pmatrix} \frac{n}{r} & 0 & 0 & 0 \\ 0 & \frac{n}{t} & 0 & 0 \\ 0 & 0 & -\frac{f+n}{f-n} & -\frac{2fn}{f-n} \\ 0 & 0 & -1 & 0 \end{pmatrix}\) 应用此矩阵到相机空间点 $(x_e, y_e, z_e, 1)$,得到裁剪空间点 $(x_c, y_c, z_c, w_c)$,其中 $w_c = -z_e$。透视除法后即可得到 NDC 坐标。
结语与延伸
本文概述了计算机图形学中的几个基础概念,包括颜色如何被感知和表示、数字图像的构成、三维物体如何用三角网格描述、如何通过光照模型模拟物体表面的明暗效果,以及如何使用变换来操纵和观察三维场景。这些是理解更高级图形学技术(如纹理映射、阴影生成、全局光照、基于物理的渲染等)的基石。
今日人物:Pat Hanrahan
提及现代计算机图形学,不能不提到 Pat Hanrahan 教授。他是斯坦福大学的教授,曾在 Pixar 担任创始员工,对 RenderMan 渲染系统做出了巨大贡献。他在光场渲染 (Light Field Rendering)、体渲染 (Volume Rendering)、GPU 编程模型等领域都有开创性工作。他荣获了包括 SIGGRAPH 成就奖、Coons 奖、奥斯卡科学技术奖以及 2019 年度的图灵奖(与 Ed Catmull 共享)在内的众多荣誉,是计算机图形学领域举足轻重的人物。他的工作极大地推动了电影特效和科学可视化的发展。
掌握了这些基础知识,你便迈出了探索精彩纷呈的计算机图形学世界的第一步。