计算机图形学基础：Bézier 曲线与曲面详解

引言

在计算机图形学的广阔领域中，三维模型和场景的设计是核心环节之一。无论是电影特效、游戏开发还是工程设计，我们都需要精确而灵活地创建和操纵复杂的几何形状。通过后续的渲染过程，例如应用渲染方程，我们可以生成具有高度真实感的图像。为了有效地完成这些三维建模任务，几何造型（Geometric Modeling） 技术应运而生，它为我们提供了描述、构建和编辑几何对象的数学工具和算法。本篇文章将深入探讨几何造型中的一个基石——Bézier 曲线与曲面。

几何造型的历史回顾

几何造型技术的发展历程中，有两个重要的里程碑：曲面造型和实体造型。

曲面造型 (Surface Modeling)

曲面造型技术在早期主要由汽车和航空工业驱动。一个标志性的贡献来自于法国雷诺汽车公司的工程师 Pierre Bézier。他在 1962 年提出了一种创新的曲线表达方式，这种方式最终演变成了我们今天熟知的 Bézier 曲线。基于此，雷诺公司于 1972 年成功开发了 UNISURF 系统，专门用于汽车表面的设计，极大地推动了计算机辅助设计（CAD）的发展。

Pierre Étienne Bézier（1910-1999）出生于法国巴黎的一个工程师世家。他于 1930 年获得机械工程学士学位，1931 年获得电子工程第二学位。值得一提的是，他在 46 年后的 1977 年获得了巴黎大学的数学博士学位。Bézier 于 1933 年加入雷诺公司，并在此工作长达 42 年。除了在工业界的卓越贡献，他还在 1968 年至 1979 年间担任国立巴黎工艺技术学院生产工程系的教授。

实体造型 (Solid Modeling)

与侧重于表示物体表面的曲面造型不同，实体造型关注于表示物体的体积信息，这对于工程分析（如有限元分析）至关重要。1973 年，剑桥大学的 Ian Braid 开发了 BUILD-1 系统，这是早期实体造型系统的代表作之一，专门用于设计工程部件。这项工作在他的博士论文 “Designing with volumes” 中有详细介绍。BUILD-1 系统的三位主要发明人也因此荣获了 2008 年的 Bézier 奖，以表彰他们在几何造型领域的开创性贡献。

如何表示曲线？

在深入 Bézier 曲线之前，我们需要了解表示曲线的几种基本数学方法。

1. 显式表示 (Explicit Representation)

在二维空间中，显式表示通常将一个变量表达为另一个变量的函数。对于 $x-y$ 平面上的曲线，可以写作 $y = f(x)$。例如，一条非垂直的直线可以表示为 $y = mx + h$。这种表示简单直观，但在处理垂直线或封闭曲线（如圆）时会遇到困难，因为一个 $x$ 值可能对应多个 $y$ 值。

2. 隐式表示 (Implicit Representation)

隐式表示通过一个方程来定义曲线，该方程描述了曲线上所有点 $(x, y)$ 必须满足的关系。在二维空间中，形式为 $f(x, y) = 0$。例如，直线可以表示为 $ax + by + c = 0$，圆心在原点的圆可以表示为 $x^2 + y^2 - r^2 = 0$。隐式表示可以方便地描述更广泛的曲线类别，并且易于判断一个点是否在曲线上。然而，直接生成曲线上的点序列（用于绘制）可能相对复杂。

3. 参数形式 (Parametric Form)

参数形式使用一个独立的参数（通常表示为 $t$）来表达曲线上点的所有坐标。随着参数 $t$ 在某个区间内变化，点的坐标 $(x(t), y(t), z(t))$ 描绘出曲线的轨迹。在三维空间中，我们有三个显式函数：

\[x = x(t) \\ y = y(t) \\ z = z(t)\]

我们可以将其写成向量形式：$P(t) = [x(t), y(t), z(t)]^T$。

参数形式具有显著的优点：

• 维度统一性：它在不同维度的空间中具有统一的表达形式。例如，从二维推广到三维，只需增加关于 $z$ 的方程即可。
• 易于绘制和处理：通过在参数区间内取一系列 $t$ 值，可以轻松生成曲线上的点序列。参数形式也适用于描述有起点和终点的曲线段。
• 表示复杂曲线：可以表示显式或隐式形式难以描述的复杂曲线，例如自相交曲线或具有特定方向性的曲线。

曲线 $P(t)$ 的导数 $P’(t) = \frac{dP(t)}{dt} = \left[\frac{dx(t)}{dt}, \frac{dy(t)}{dt}, \frac{dz(t)}{dt}\right]^T$ 表示曲线在该点的切向量，其方向是曲线的切线方向，其模长 $|P’(t)|$ 可以被视为参数 $t$ 变化时点在曲线上移动的“速率”。

参数多项式曲线

参数曲线的一种重要形式是参数多项式曲线，其中 $x(t), y(t), z(t)$ 都是关于参数 $t$ 的多项式函数。一个典型的例子是三阶（三次）参数多项式曲线：

\[P(t) = \mathbf{a}t^3 + \mathbf{b}t^2 + \mathbf{c}t + \mathbf{d}\]

其中 $\mathbf{a}, \mathbf{b}, \mathbf{c}, \mathbf{d}$ 是向量系数。这种形式也被称为 Ferguson 曲线，曾在美国早期的飞机设计中使用。然而，Ferguson 曲线的一个主要缺点是其不直观性：给定系数 $\mathbf{a}, \mathbf{b}, \mathbf{c}, \mathbf{d}$ 后，很难直接想象出曲线的形状，这给交互式设计带来了困难。

Bézier 曲线: 概念及性质

正是为了解决参数多项式曲线不直观的问题，Pierre Bézier 提出了一种基于“控制点”的曲线构造方法。

Bézier 的原始思想与 Forrest 的改进

Bézier 最初提出使用一系列“连接向量”（connected vectors）的加权和来表示曲线。其原始定义（使用 $V_i(t)$ 和 $A_i(t)$ 函数）相对复杂，不易理解：

\[P(t) = \sum_{i=0}^{n} V_i(t) f_i(t)\]

其中 $f_i(t)$ 基于 $A_j(t)$ 的积分形式，而 $A_j(t)$ 又依赖于 $t^j (1-t)^{n-j}$ 的导数。这种形式虽然具有数学上的完备性，但对于设计者来说不够直观。

一个关键的转折点发生在 1972 年，A. R. Forrest 在《Computer Aided Design》杂志上发表了一篇影响深远的论文。他指出，Bézier 提出的曲线可以更简洁、更直观地通过 伯恩斯坦多项式 (Bernstein Polynomials) 在一组控制点 (Control Points) 上定义。这一发现极大地促进了 Bézier 曲线的理解和应用。

值得一提的是，中国学者如梁友栋、刘鼎元、常庚哲等也在相关领域做出了重要贡献。为了纪念 Bézier 教授（于 1999 年去世），国际权威期刊《Computer Aided Geometric Design》(CAGD) 在 2001 年为他出版了一期特刊。

Bézier 曲线的定义

给定 $n+1$ 个控制点 $P_0, P_1, \ldots, P_n$，一条 $n$ 次 Bézier 曲线 $P(t)$ 定义为：

\[P(t) = \sum_{i=0}^{n} P_i B_{i,n}(t), \quad t \in [0, 1]\]

其中 $P_i$ 是控制顶点，$B_{i,n}(t)$ 是第 $i$ 个 $n$ 阶 Bernstein 基函数 (Bernstein Basis Function)，定义为：

\[B_{i,n}(t) = \binom{n}{i} t^i (1-t)^{n-i} = \frac{n!}{i!(n-i)!} t^i (1-t)^{n-i}, \quad i = 0, 1, \ldots, n\]

这里 $\binom{n}{i}$ 是二项式系数。

控制点 $P_0, P_1, \ldots, P_n$ 顺次连接构成的折线称为控制多边形 (Control Polygon) 或控制网格 (Control Net)。Bézier 曲线的形状完全由其控制点的位置决定。通过移动控制点，设计者可以直观地、交互式地修改曲线的形状。

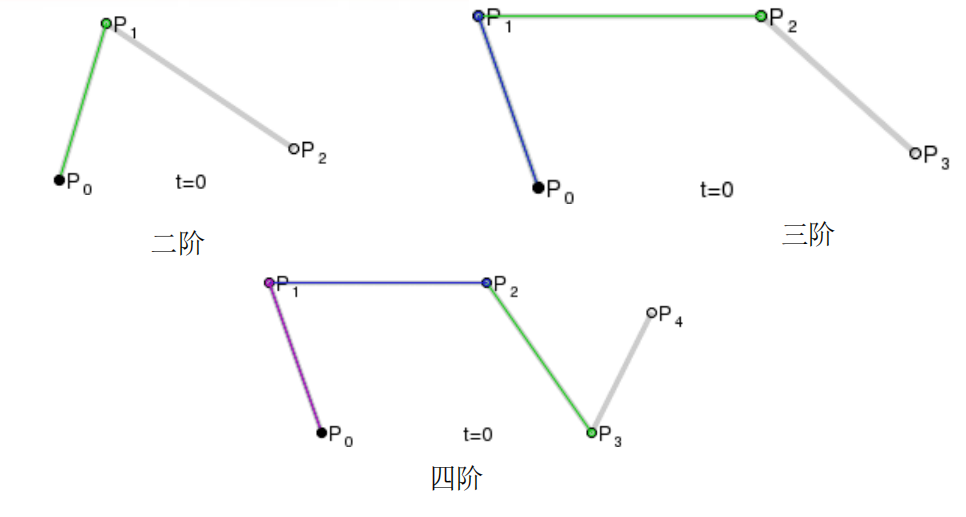
下面是低阶 Bézier 曲线的例子：

• 二阶 (Quadratic): $P(t) = P_0 B_{0,2}(t) + P_1 B_{1,2}(t) + P_2 B_{2,2}(t) = P_0 (1-t)^2 + P_1 2t(1-t) + P_2 t^2$
• 三阶 (Cubic): $P(t) = \sum_{i=0}^3 P_i B_{i,3}(t) = P_0 (1-t)^3 + P_1 3t(1-t)^2 + P_2 3t^2(1-t) + P_3 t^3$
• 四阶 (Quartic): $P(t) = \sum_{i=0}^4 P_i B_{i,4}(t)$

Bernstein 多项式的性质

Bézier 曲线的许多重要性质源于 Bernstein 基函数的性质。

1. 非负性 (Non-negativity): 对于 $t \in [0, 1]$ 和 $i = 0, 1, \ldots, n$，有 $B_{i,n}(t) \ge 0$。

2. 端点性质 (End Point Property):

   \[B_{i,n}(0) = \begin{cases} 1 & \text{if } i=0 \\ 0 & \text{if } i>0 \end{cases}\] \[B_{i,n}(1) = \begin{cases} 1 & \text{if } i=n \\ 0 & \text{if } i<n \end{cases}\]

3. 归一性 (Partition of Unity): 对于 $t \in [0, 1]$，所有 Bernstein 基函数之和恒为 1：

   \[\sum_{i=0}^{n} B_{i,n}(t) \equiv 1\]

   证明：根据二项式定理 $(x+y)^n = \sum_{i=0}^n \binom{n}{i} x^i y^{n-i}$，令 $x=t, y=1-t$，即可得到 $\sum_{i=0}^{n} \binom{n}{i} t^i (1-t)^{n-i} = (t + (1-t))^n = 1^n = 1$。

4. 对称性 (Symmetry): 基函数关于 $i$ 和 $n-i$ 以及 $t$ 和 $1-t$ 对称：

   \[B_{i,n}(t) = B_{n-i,n}(1-t)\]

   证明： $B_{n-i,n}(1-t) = \binom{n}{n-i} (1-t)^{n-i} (1-(1-t))^{n-(n-i)} = \binom{n}{i} (1-t)^{n-i} t^i = B_{i,n}(t)$。

5. 递归性 (Recursion): $n$ 阶 Bernstein 基函数可以由两个 $n-1$ 阶基函数线性组合得到：

   \[B_{i,n}(t) = (1-t) B_{i,n-1}(t) + t B_{i-1,n-1}(t), \quad i=0, 1, \ldots, n\]

   (约定 $B_{-1,n-1}(t) = 0$ 和 $B_{n,n-1}(t) = 0$)。这个性质是 de Casteljau 算法的基础。 证明：

   \[\begin{aligned} &(1-t) B_{i,n-1}(t) + t B_{i-1,n-1}(t) \\ &= (1-t) \binom{n-1}{i} t^i (1-t)^{n-1-i} + t \binom{n-1}{i-1} t^{i-1} (1-t)^{n-1-(i-1)} \\ &= \binom{n-1}{i} t^i (1-t)^{n-i} + \binom{n-1}{i-1} t^i (1-t)^{n-i} \\ &= \left[ \binom{n-1}{i} + \binom{n-1}{i-1} \right] t^i (1-t)^{n-i} \\ &= \binom{n}{i} t^i (1-t)^{n-i} = B_{i,n}(t) \quad \text{(使用了帕斯卡法则 } \binom{n-1}{i} + \binom{n-1}{i-1} = \binom{n}{i}) \end{aligned}\]

6. 导数 (Derivative): Bernstein 基函数的导数可以表示为两个低一阶的 Bernstein 基函数的差：

   \[\frac{d}{dt} B_{i,n}(t) = B'_{i,n}(t) = n (B_{i-1,n-1}(t) - B_{i,n-1}(t)), \quad i = 0, 1, \ldots, n\]

   (同样约定 $B_{-1,n-1}(t) = 0$ 和 $B_{n,n-1}(t) = 0$)。

7. 最大值 (Maximum Value): $B_{i,n}(t)$ 在 $t = i/n$ 处达到其在区间 $[0, 1]$ 上的唯一最大值。

8. 升阶 (Degree Raising) 公式: 一个 $n$ 阶 Bernstein 基函数可以精确地表示为两个 $n+1$ 阶基函数的线性组合：

   \[(1-t)B_{i,n}(t) = (1-\frac{i}{n+1}) B_{i,n+1}(t)\] \[tB_{i,n}(t) = \frac{i+1}{n+1} B_{i+1,n+1}(t)\] \[B_{i,n}(t) = (1 - \frac{i}{n+1}) B_{i,n+1}(t) + \frac{i+1}{n+1} B_{i+1,n+1}(t)\]

9. 积分 (Integral): Bernstein 基函数在 $[0, 1]$ 上的定积分很简单：

   \[\int_{0}^{1} B_{i,n}(t) dt = \frac{1}{n+1}\]

Bézier 曲线的性质

基于 Bernstein 基函数的性质，Bézier 曲线具有以下重要几何性质：

1. 端点插值性 (End Point Interpolation): 曲线的起点和终点分别与控制多边形的第一个和最后一个顶点重合。 根据 Bernstein 基函数的端点性质： $P(0) = \sum_{i=0}^{n} P_i B_{i,n}(0) = P_0 \cdot 1 + \sum_{i=1}^{n} P_i \cdot 0 = P_0$ $P(1) = \sum_{i=0}^{n} P_i B_{i,n}(1) = \sum_{i=0}^{n-1} P_i \cdot 0 + P_n \cdot 1 = P_n$

2. 切向量 (Tangent Vector): 曲线在端点处的切向量方向与控制多边形相应端点的边的方向一致。 曲线的导数（切向量）为：

   \[P'(t) = \frac{d}{dt} \sum_{i=0}^{n} P_i B_{i,n}(t) = \sum_{i=0}^{n} P_i B'_{i,n}(t) = \sum_{i=0}^{n} P_i n (B_{i-1,n-1}(t) - B_{i,n-1}(t))\]

   通过调整求和下标，可以得到更简洁的形式：

   \[P'(t) = n \sum_{i=0}^{n-1} (P_{i+1} - P_i) B_{i,n-1}(t)\]

   令 $t=0$ 和 $t=1$，并利用 Bernstein 基函数的端点性质： $P’(0) = n \sum_{i=0}^{n-1} (P_{i+1} - P_i) B_{i,n-1}(0) = n (P_1 - P_0) \cdot 1 = n(P_1 - P_0)$ $P’(1) = n \sum_{i=0}^{n-1} (P_{i+1} - P_i) B_{i,n-1}(1) = n (P_n - P_{n-1}) \cdot 1 = n(P_n - P_{n-1})$ 这表明，起点处的切线方向平行于向量 $P_1 - P_0$（控制多边形的第一条边），终点处的切线方向平行于向量 $P_n - P_{n-1}$（控制多边形的最后一条边）。系数 $n$ 影响切向量的长度。

3. 二阶导数 (Second Derivative): 曲线的二阶导数为：

   \[P''(t) = n(n-1) \sum_{i=0}^{n-2} (P_{i+2} - 2P_{i+1} + P_i) B_{i,n-2}(t)\]

   在端点处： $P’‘(0) = n(n-1) (P_2 - 2P_1 + P_0)$ $P’‘(1) = n(n-1) (P_n - 2P_{n-1} + P_{n-2})$ 二阶导数与曲线的曲率相关。例如，端点处的曲率 $k$ 可以通过 $k = \frac{|P’(t) \times P’‘(t)|}{|P’(t)|^3}$ 计算。将 $t=0$ 和 $t=1$ 时的 $P’$ 和 $P’’$ 代入，可得端点曲率的表达式，例如在 $t=0$ 处：

   \[k(0) = \frac{\| n(P_1 - P_0) \times n(n-1)(P_2 - 2P_1 + P_0) \|}{\|n(P_1 - P_0)\|^3} = \frac{n-1}{n} \frac{\|(P_1 - P_0) \times (P_2 - P_1)\|}{\|P_1 - P_0\|^3}\]

   这表明端点曲率仅由前三个（或后三个）控制点决定。

4. k 阶导数的差分形式: 曲线的 $k$ 阶导数可以用控制点的前向差分向量 $\Delta^k P_i$ 来表示：

   \[P^{(k)}(t) = \frac{n!}{(n-k)!} \sum_{i=0}^{n-k} \Delta^k P_i B_{i,n-k}(t), \quad t \in [0, 1]\]

   其中前向差分向量递归定义： $\Delta^0 P_i = P_i$ $\Delta^k P_i = \Delta^{k-1} P_{i+1} - \Delta^{k-1} P_i$, for $k \ge 1$. 例如，$\Delta^1 P_i = P_{i+1} - P_i$，$\Delta^2 P_i = (P_{i+2} - P_{i+1}) - (P_{i+1} - P_i) = P_{i+2} - 2P_{i+1} + P_i$。这与前面 $P’(t)$ 和 $P’‘(t)$ 的表达式一致。

5. 对称性 (Symmetry): 如果将控制点序列逆序排列，即 $P_i^* = P_{n-i}$ ($i=0, \ldots, n$)，得到的新 Bézier 曲线 $P^*(t)$ 与原曲线 $P(t)$ 具有相同的形状，但参数化的方向相反：

   \[P^*(t) = \sum_{i=0}^{n} P_i^* B_{i,n}(t) = \sum_{i=0}^{n} P_{n-i} B_{i,n}(t)\]

   利用 Bernstein 基函数的对称性 $B_{i,n}(t) = B_{n-i,n}(1-t)$，令 $j=n-i$，则 $i=n-j$：

   \[P^*(t) = \sum_{j=0}^{n} P_j B_{n-j,n}(t) = \sum_{j=0}^{n} P_j B_{j,n}(1-t) = P(1-t)\]

   因此，$P^*(t)$ 描绘的几何路径与 $P(t)$ 相同，只是起点和终点互换了。

6. 凸包性 (Convex Hull Property): Bézier 曲线完全包含在其控制点 $P_0, \ldots, P_n$ 构成的凸包 (Convex Hull) 内。 这是因为对于 $t \in [0, 1]$，Bernstein 基函数满足 $B_{i,n}(t) \ge 0$ 且 $\sum_{i=0}^{n} B_{i,n}(t) = 1$。因此，曲线上的每一点 $P(t)$ 都是控制点的一个凸组合 (convex combination)，根据凸组合的定义，该点必在这些控制点的凸包内部或边界上。 （此处可插入展示 Bézier 曲线及其控制点凸包的图像，如图 3.1.9）
7. 几何不变性 (Geometric Invariance): Bézier 曲线的形状仅依赖于其控制点 $P_i$ 的相对位置，而与坐标系的选择无关。对所有控制点进行相同的仿射变换（如平移、旋转、缩放），得到的曲线是原曲线经过相同仿射变换后的结果。

de Casteljau 算法

虽然 Bézier 曲线的定义式给出了曲线的数学表达，但在实际应用中，直接计算高阶 Bernstein 多项式的值可能存在数值稳定性问题，且计算量较大。为了高效且稳定地计算 Bézier 曲线上给定参数 $t$ 处的点 $P(t)$，Paul de Casteljau（另一位在雷诺公司工作的工程师，他的工作早于 Bézier 但发表较晚）提出了一种优雅的递归算法。

de Casteljau 算法的核心思想是利用 Bernstein 基函数的递归性质。回忆 $B_{i,n}(t) = (1-t) B_{i,n-1}(t) + t B_{i-1,n-1}(t)$。将其代入 Bézier 曲线定义并整理可以得到：

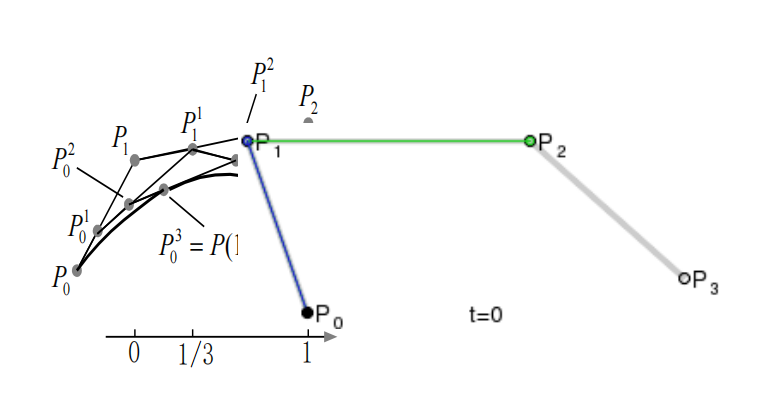
\[P(t) = \sum_{i=0}^{n} P_i B_{i,n}(t) = \sum_{i=0}^{n-1} \underbrace{[(1-t)P_i + t P_{i+1}]}_{P_i^1(t)} B_{i,n-1}(t)\]

这表明，原始的 $n$ 次 Bézier 曲线可以看作是由 $n$ 个新的控制点 $P_0^1(t), \ldots, P_{n-1}^1(t)$ 定义的 $n-1$ 次 Bézier 曲线。其中，每个新控制点 $P_i^1(t)$ 都是原相邻控制点 $P_i$ 和 $P_{i+1}$ 沿它们之间的连线段按比例 $t:(1-t)$ 进行线性插值得到的结果。

重复这个过程 $n$ 次，每次都将前一步得到的 $k$ 个控制点 $P_0^{n-k}, \ldots, P_{k-1}^{n-k}$ 通过线性插值生成 $k-1$ 个新的控制点 $P_0^{n-k+1}, \ldots, P_{k-2}^{n-k+1}$，直到最后只剩下一个点 $P_0^n(t)$。这个最终的点就是曲线上参数 $t$ 对应的点 $P(t)$。

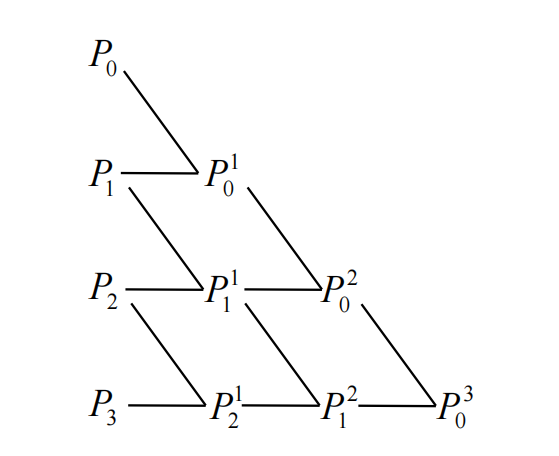
de Casteljau 算法的递推公式： 设 $P_i^0 = P_i$ ($i = 0, \ldots, n$)。 对于 $k = 1, \ldots, n$，计算：

\[P_i^k(t) = (1-t) P_i^{k-1}(t) + t P_{i+1}^{k-1}(t), \quad i = 0, \ldots, n-k\]

最终结果为 $P(t) = P_0^n(t)$。

这个过程可以用一个三角形计算格式直观表示。以 $n=3$ 为例：

de Casteljau 算法不仅数值稳定，而且具有重要的几何意义：中间计算得到的点 $P_i^k(t)$ 构成了更低阶 Bézier 曲线的控制点，并且 $P_0^k(t)$ 和 $P_{n-k}^k(t)$ 分别是原始曲线在 $[0, t]$ 和 $[t, 1]$ 区间上进行参数分割后得到的两段 $n$ 次 Bézier 曲线的控制点序列的最后一个和第一个点。

de Casteljau 的历史贡献：他被认为是提出了三个在曲面造型中至关重要的基本思想：1) 使用 Bernstein 多项式作为参数化多项式曲线和曲面的基函数；2) 使用多线性多项式（即 de Casteljau 算法的递推形式）作为这些多项式的表示，为理解和使用样条提供了基础工具；3) 利用这种多线性形式给出了一个高效且稳定的求值算法。

---

思考题 (单选题 1分)

一条 3 次 Bézier 曲线的控制顶点为 $P_0=(10,0)$, $P_1=(30,60)$, $P_2=(130,60)$, $P_3=(190, 0)$。请问当参数 $t=1/2$ 时，曲线上的点 $P(1/2)$ 的坐标是多少？

A. (85, 30) B. (100, 45) C. (85, 45) D. (100, 30)

• 解题思路: 应用 de Casteljau 算法，计算 $t=1/2$ 时的点。
  • $P_0^1 = (1/2)P_0 + (1/2)P_1 = (1/2)(10,0) + (1/2)(30,60) = (5,0) + (15,30) = (20, 30)$
  • $P_1^1 = (1/2)P_1 + (1/2)P_2 = (1/2)(30,60) + (1/2)(130,60) = (15,30) + (65,30) = (80, 60)$
  • $P_2^1 = (1/2)P_2 + (1/2)P_3 = (1/2)(130,60) + (1/2)(190,0) = (65,30) + (95,0) = (160, 30)$
  • $P_0^2 = (1/2)P_0^1 + (1/2)P_1^1 = (1/2)(20,30) + (1/2)(80,60) = (10,15) + (40,30) = (50, 45)$
  • $P_1^2 = (1/2)P_1^1 + (1/2)P_2^1 = (1/2)(80,60) + (1/2)(160,30) = (40,30) + (80,15) = (120, 45)$
  • $P_0^3 = P(1/2) = (1/2)P_0^2 + (1/2)P_1^2 = (1/2)(50,45) + (1/2)(120,45) = (25, 22.5) + (60, 22.5) = (85, 45)$
• 答案: C

---

几何连续性

在实际的 CAD 应用中，通常不鼓励使用非常高阶的 Bézier 曲线来拟合复杂的形状，因为高阶曲线难以控制，且可能出现不必要的振荡。更常用的方法是使用多段低阶（通常是二次或三次）Bézier 曲线拼接而成。这就引出了曲线段之间如何光滑连接的问题。

我们通常使用的函数连续性概念（$C^0, C^1, C^2, \ldots$）在几何造型中可能并不完全适用。$C^k$ 连续性要求曲线在连接点处的直到 $k$ 阶的导数都相等。然而，仅仅参数导数的相等并不能完全反映几何形状上的光滑性。

考虑一个例子：

\[\Phi(t) = \begin{cases} V_0 + \frac{V_1 - V_0}{3} t, & 0 \leq t \leq 1 \\ V_0 + \frac{V_1 - V_0}{3} + (t-1) \frac{2(V_1 - V_0)}{3}, & 1 < t \leq 2 \end{cases}\]

导数在 $t=1$ 两侧为：

\[\Phi'(1^-) = \frac{1}{3}(V_1 - V_0)\] \[\Phi'(1^+) = \frac{2}{3}(V_1 - V_0)\]

这意味着该导数 $\Phi’(t)$ 在 $t=1$ 处不连续，即 $||\Phi’(1^-)||^2 \neq ||\Phi’(1^+)||^2$。但这条曲线本身就是一条直线。

这个现象表明，传统的函数连续性对于描述 CAD 和图形学中形状的视觉光滑性来说过于严格。因此，引入了 几何连续性 (Geometric Continuity) 的概念，记作 $G^k$。几何连续性关注的是曲线本身的几何属性（如切线方向、曲率）在连接点处的连续性，而不要求参数导数本身完全相等。中国学者刘鼎元和梁友栋在几何连续性理论方面有重要贡献。

$G^n$ 几何连续性条件

对于两条 Bézier 曲线 $P(t)$（控制点 $P_0, \ldots, P_n$）和 $Q(t)$（控制点 $Q_0, \ldots, Q_m$），它们在 $P(1) = Q(0)$ 处连接：

• $G^0$ 连续 (位置连续): 两条曲线的连接点重合。

  \[P_n = Q_0\]

• $G^1$ 连续 (切线连续): 在连接点处，$G^0$ 连续，并且两条曲线在该点有共同的切线方向（允许切向量长度不同）。对于 Bézier 曲线，这等价于连接点和它两旁的控制点三点共线。

  \[P_n = Q_0 \quad \text{and} \quad P_n - P_{n-1} = \alpha (Q_1 - Q_0) \quad \text{for some } \alpha > 0\]

  这意味着 $P_{n-1}, P_n(=Q_0), Q_1$ 三点共线，且 $P_n(=Q_0)$ 位于 $P_{n-1}$ 和 $Q_1$ 之间。$\alpha$ 是切向量长度的比值。

• $G^2$ 连续 (曲率连续): 在连接点处，$G^1$ 连续，并且两条曲线在该点有相同的曲率。对于 Bézier 曲线，这需要满足一个更复杂的涉及 $P_{n-2}, P_{n-1}, P_n, Q_1, Q_2$ 以及 $G^1$ 条件中的比例因子 $\alpha$ 的关系式。

  \[P_n = Q_0, \quad P_n - P_{n-1} = \alpha (Q_1 - Q_0) \quad (\alpha > 0)\]

  并且（假设 $P, Q$ 都是 $n$ 次曲线）:

  \[Q_2 = \alpha^2 P_{n-2} - (2\alpha + 2\alpha^2 + \frac{\beta}{n-1}) P_{n-1} + (1 + 2\alpha + \alpha^2 + \frac{\beta}{n-1}) P_n\]

  或者更常见的形式是要求二阶导数向量共面且满足特定比例关系：

  \[Q''(0) = \alpha^2 P''(1) + \beta Q'(1) \quad \text{for some } \beta\]

  代入 Bézier 曲线的导数表达式，可以得到关于控制点的具体条件。例如，当 $\alpha=1$ 时（即 $C^1$ 连续），$G^2$ 连续要求 $Q_2 - 2Q_1 + Q_0 = P_n - 2P_{n-1} + P_{n-2}$，即 $C^2$ 连续。

几何连续性提供了比函数连续性更灵活的控制，允许在保持视觉光滑的同时调整曲线段的参数化。

升阶 (Degree Raising/Elevation)

有时，我们可能需要增加一条 Bézier 曲线的次数，但保持其几何形状和参数化不变。这个过程称为升阶。升阶的主要目的可能包括：

• 为曲线增加更多的控制点，从而提供更灵活的形状调整能力。
• 在与其他更高次曲线进行运算（如求交）或连接时，统一曲线的次数。

一条 $n$ 次 Bézier 曲线 $P(t) = \sum_{i=0}^n P_i B_{i,n}(t)$ 可以精确地表示为一条 $n+1$ 次 Bézier 曲线 $P(t) = \sum_{i=0}^{n+1} P_i^* B_{i,n+1}(t)$。新的 $n+2$ 个控制点 $P_0^*, \ldots, P_{n+1}^*$ 可以通过以下公式从旧的 $n+1$ 个控制点 $P_0, \ldots, P_n$ 计算得到：

\[P_i^* = \frac{i}{n+1} P_{i-1} + \left(1 - \frac{i}{n+1}\right) P_i, \quad i = 0, 1, \ldots, n+1\]

这个公式表明，新的控制点 $P_i^*$ 是旧的相邻控制点 $P_{i-1}$ 和 $P_i$ 的一个凸组合（系数为 $\frac{i}{n+1}$ 和 $1 - \frac{i}{n+1}$，它们非负且和为 1）。

升阶具有以下特点：

• 新的控制多边形 $P_0^*, \ldots, P_{n+1}^*$ 仍然包围着原曲线。
• 新的控制多边形通常比旧的控制多边形更靠近曲线。
• 重复升阶过程，控制多边形会收敛于 Bézier 曲线本身。

降阶 (Degree Reduction)

降阶是升阶的逆过程：给定一条 $n$ 次 Bézier 曲线（由 $P_0, \ldots, P_n$ 定义），我们希望找到一条 $n-1$ 次 Bézier 曲线（由 $P_0^{*}, \ldots, P_{n-1}^{*}$ 定义），使其尽可能地逼近原始曲线。

与升阶不同，降阶通常是一个近似过程，除非原始的 $n$ 次曲线本身就是由一条 $n-1$ 次曲线升阶得到的。精确降阶只有在特定条件下才可能。

降阶的目标是找到一组新的控制点 $P_i^{*}$ ($i=0, \ldots, n-1$)，使得它们定义的 $n-1$ 次曲线 $P^{*}(t) = \sum_{i=0}^{n-1} P_i^{*} B_{i,n-1}(t)$ 与原始曲线 $P(t)$ 之间的误差（例如，在某种范数意义下的距离）最小。

可以通过升阶公式的反向关系来推导降阶的近似方法。假设 $P_i$ 是 $P_i^*$ 升阶的结果，则有：

\[P_i = \frac{n-i}{n} P_{i}^* + \frac{i}{n} P_{i-1}^*\]

我们可以得到两个递推公式

\[P_i^{\sharp} = \frac{nP_i-iP_{i-1}^{\sharp}}{n-i}, i=0,1,\ldots,n-1\] \[P_{i-1}^* = \frac{nP_i-(n-i)P_i^*}{i}, i=n,n-1,\ldots,1\]

于是，有两种基于端点信息的近似降阶方案：

1. Forrest (1972)

   \[\hat{P}_{i}=\left\{\begin{array}{ll} P_{i}^{\sharp}, & i=0,1, \cdots,\left[\frac{n-1}{2}\right] \\ P_{i}^{*}, & i=\left[\frac{n-1}{2}\right]+1, \cdots, n-1 \end{array}\right.\]

2. Farin (1983)

   \[\hat{P}_{i}=\left(1-\frac{i}{n-1}\right) P_{i}^{\sharp}+\frac{i}{n-1} P_{i}^{*}\]

这两种方法通常得到不同的结果。更复杂的降阶方法会试图在某种全局最优意义下（如最小二乘）找到最佳的 $n-1$ 次逼近曲线。

相关参考文献:

• M. A. Watkins and A. J. Worsey, “Degree reduction of Bézier curves”, Computer Aided Design, 20(7), 1988, 398-405.
• 胡事民、孙家广、金通洸等, “Approximate degree reduction of Bézier curves”, Tsinghua Science and Technology, No.2, 1998, 997-1000. (Reported in national CAGD conference, 1993).
• 雍俊海、胡事民、孙家广等, “Degree reduction of B-spline curves”, Computer Aided Geometric Design, Vol. 13, No. 2, 2001, 117-127.

Bézier 曲面

Bézier 曲线的概念可以自然地推广到曲面，用于在三维空间中定义和控制更复杂的形状。主要有两种类型的 Bézier 曲面：定义在矩形域上的和定义在三角域上的。

矩形域 Bézier 曲面 (Rectangular Bézier Surface)

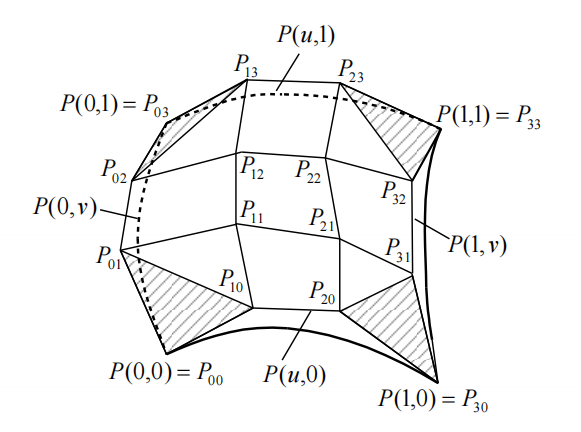
一个 $m \times n$ 次的矩形域 Bézier 曲面由 $(m+1) \times (n+1)$ 个控制点 $P_{ij}$ ($i=0,\ldots,m; j=0,\ldots,n$) 排列成的网格定义。曲面上的点 $P(u, v)$ 通过 张量积 (Tensor Product) 的形式给出，其中参数 $u, v \in [0, 1]$：

\[P(u, v) = \sum_{i=0}^{m} \sum_{j=0}^{n} P_{ij} B_{i,m}(u) B_{j,n}(v)\]

这里 $B_{i,m}(u)$ 是 $m$ 阶 Bernstein 基函数， $B_{j,n}(v)$ 是 $n$ 阶 Bernstein 基函数。

矩阵表达: 该定义可以写成矩阵形式：

\[P(u, v) = \mathbf{U} \mathbf{P} \mathbf{V}^T\]

其中： $\mathbf{U} = [B_{0,m}(u), B_{1,m}(u), \ldots, B_{m,m}(u)]$

$\mathbf{P} = \begin{pmatrix} P_{00} & P_{01} & \cdots & P_{0n} \\ P_{10} & P_{11} & \cdots & P_{1n} \\ \vdots & \vdots & \ddots & \vdots \\ P_{m0} & P_{m1} & \cdots & P_{mn} \end{pmatrix}$

$\mathbf{V} = [B_{0,n}(v), B_{1,n}(v), \ldots, B_{n,n}(v)]^T$

矩形域 Bézier 曲面的性质: 矩形域 Bézier 曲面继承了 Bézier 曲线的许多优良性质：

• 角点插值: 曲面的四个角点与控制网格的四个角点重合： $P(0,0) = P_{00}$ $P(1,0) = P_{m0}$ $P(0,1) = P_{0n}$ $P(1,1) = P_{mn}$
• 边界曲线: 曲面的四条边界线是 Bézier 曲线。例如，当 $v=0$ 时，$P(u, 0) = \sum_{i=0}^m P_{i0} B_{i,m}(u)$ 是一条由第一行控制点 $P_{00}, \ldots, P_{m0}$ 定义的 Bézier 曲线。类似地，$u=0, u=1, v=1$ 时也对应 Bézier 边界曲线。
• 切平面: 在四个角点处的切平面由相应的角点及其相邻的两个控制点确定。例如，在 $P(0,0)=P_{00}$ 处，切平面由 $P_{00}, P_{10}, P_{01}$ 三点确定。
• 几何不变性: 曲面形状仅依赖于控制点相对位置，与坐标系无关。
• 对称性: (如果 $m=n$, 控制网格对称，则曲面也可能具有对称性)。
• 凸包性: 曲面完全包含在其控制点构成的凸包内。

几何连续性: 两个 $m \times n$ 次的矩形域 Bézier 曲面 $P(u,v)$ (控制点 $P_{ij}$) 和 $Q(u,v)$ (控制点 $Q_{ij}$) 可以沿着一条公共边界光滑拼接。假设它们沿着 $v=1$ (对于 $P$) 和 $v=0$ (对于 $Q$) 的边界连接。

• $G^0$ 连续: 要求公共边界上的点重合。

  \[P(u, 1) = Q(u, 0) \quad \text{for all } u \in [0, 1]\]

  这等价于要求对应边界行的控制点完全相同：

  \[P_{i,n} = Q_{i,0}, \quad i = 0, \ldots, m\]

• $G^1$ 连续: 在 $G^0$ 的基础上，要求在公共边界上每一点的切平面是连续的。这等价于跨界切向量 $\frac{\partial P}{\partial v}(u, 1)$ 和 $\frac{\partial Q}{\partial v}(u, 0)$ 在每一点 $u$ 处方向相同（共线），并且指向同一个法向侧。

  \[\frac{\partial Q}{\partial v}(u, 0) = \alpha(u) \frac{\partial P}{\partial v}(u, 1) + \beta(u) \frac{\partial P}{\partial u}(u, 1) \quad (?)\]

  更常见的 $G^1$ 条件是（对于 Bézier 曲面）：

  \[Q_{i,1} - Q_{i,0} = \alpha_i (P_{i,n} - P_{i,n-1}) \quad \text{for some } \alpha_i > 0, \quad i = 0, \ldots, m\]

  如果要求 $\alpha_i$ 对于所有 $i$ 都等于同一个常数 $\alpha > 0$，则连接处是 $C^1$ 连续的。如果 $\alpha_i$ 可以随 $i$ 变化，则是 $G^1$ 连续。这意味着 $P_{i,n-1}, P_{i,n}(=Q_{i,0}), Q_{i,1}$ 对于每个 $i$ 都是共线的。

de Casteljau 算法: Bézier 曲线的 de Casteljau 算法可以推广到矩形域曲面，用于计算 $P(u,v)$。可以分两步进行：

1. 对控制点矩阵 $\mathbf{P}$ 的每一行 $P_{i0}, \ldots, P_{in}$，应用关于参数 $v$ 的 de Casteljau 算法，得到 $m+1$ 个点 $P_i(v) = \sum_{j=0}^n P_{ij} B_{j,n}(v)$。
2. 对这 $m+1$ 个点 $P_0(v), \ldots, P_m(v)$，应用关于参数 $u$ 的 de Casteljau 算法，最终得到 $P(u,v) = \sum_{i=0}^m P_i(v) B_{i,m}(u)$。

或者，可以使用一个统一的递归公式。

\[\begin{array}{l} P(u, v)=\sum_{i=0}^{m-k} \sum_{j=0}^{n-l} P_{i, j}^{k, l} B_{i, m}(u) B_{j, n}(v)=\cdots=P_{00}^{m . n} \\ u, v \in[0,1] \end{array}\] \[\begin{array}{l} P_{i, j}^{k, l}=\left\{\begin{array}{cc} P_{i j} & (k=l=0) \\ (1-u) P_{i j}^{k-1,0}+u P_{i+1, j}^{k-1,0} & (k=1,2, \cdots, m ; l=0) \\ (1-v) P_{0, j}^{m, l-1}+v P_{0, j+1}^{m, l-1} & (k=m, l=1,2, \cdots, n) \end{array}\right.\\ P_{i j}^{k, l}=\left\{\begin{array}{cc} P_{i j} & (k=l=0) \\ (1-v) P_{i j}^{0, l-1}+v P_{i, j+1}^{0, l-1} & (k=0 ; l=1,2, \cdots, n) \\ (1-u) P_{i 0}^{k-1, n}+u P_{i+1,0}^{k+1, n} & (k=1,2, \cdots, m ; l=n) \end{array}\right. \end{array}\]

de Casteljau 算法的直观解释：

\[\begin{aligned} P(u, v) & =\sum_{i=0}^{m} \sum_{j=0}^{n} P_{i j} B_{i, m}(u) B_{j, n}(v) \\ & =\sum_{i=0}^{m}\left(\sum_{j=0}^{n} P_{i j} B_{j, n}(v)\right) B_{i, m}(u) \end{aligned}\]

三角域 Bézier 曲面 (Triangular Bézier Surface)

有时，几何模型的某些部分天然地具有三角形拓扑结构，例如在有限元网格或某些设计场景中。在这种情况下，使用定义在三角域上的 Bézier 曲面更为自然。

三角域 Bézier 曲面使用 重心坐标 (Barycentric Coordinates) $(u, v, w)$ 来参数化三角形域内的点。对于一个参考三角形（例如，顶点为 $(1,0,0), (0,1,0), (0,0,1)$ 的重心坐标空间），域内的点满足 $u+v+w = 1$ 且 $u, v, w \ge 0$。

Bernstein 基函数 (三角域): $n$ 次三角域 Bézier 曲面的基函数是定义在重心坐标上的多元 Bernstein 多项式：

\[B_{i,j,k}^n(u, v, w) = \frac{n!}{i! j! k!} u^i v^j w^k\]

其中 $i, j, k$ 是非负整数，且 $i+j+k=n$。 总共有 $\binom{n+2}{2} = \frac{(n+1)(n+2)}{2}$ 个这样的基函数。 这些基函数也具有非负性、归一性 ($\sum_{i+j+k=n} B_{i,j,k}^n(u,v,w) = 1$) 和递归性质：

\[B_{i,j,k}^n(u,v,w) = u B_{i-1,j,k}^{n-1}(u,v,w) + v B_{i,j-1,k}^{n-1}(u,v,w) + w B_{i,j,k-1}^{n-1}(u,v,w)\]

(约定当任何下标为负时，基函数为 0)。

三角域 Bézier 曲面的定义: 一个 $n$ 次三角域 Bézier 曲面由 $\frac{(n+1)(n+2)}{2}$ 个控制点 $P_{ijk}$ ($i+j+k=n$) 定义，这些控制点通常排列成一个三角形网格。曲面定义为：

\[P(u, v, w) = \sum_{i+j+k=n} P_{ijk} B_{i,j,k}^n(u, v, w)\]

其中 $u+v+w=1, u,v,w \ge 0$。

de Casteljau 算法 (三角域): 与矩形域类似，三角域 Bézier 曲面也有对应的 de Casteljau 算法。令 $P_{ijk}^0 = P_{ijk}$。 对于 $l = 1, \ldots, n$，计算：

\[P_{ijk}^l(u,v,w) = u P_{i+1,j,k}^{l-1}(u,v,w) + v P_{i,j+1,k}^{l-1}(u,v,w) + w P_{i,j,k+1}^{l-1}(u,v,w)\]

(这里 $i+j+k = n-l$)。 最终结果为 $P(u,v,w) = P_{000}^n(u,v,w)$。

三角域 Bézier 曲面同样具有凸包性、几何不变性等性质。其边界是 Bézier 曲线。例如，当 $w=0$ 时，$u+v=1$，曲面退化为一条由控制点 $P_{i,j,0}$ ($i+j=n$) 定义的 $n$ 次 Bézier 曲线（参数为 $u$ 或 $v$）。

矩形域与三角域 Bézier 曲面的转换

在同一个 CAD 系统中，可能同时需要处理矩形域和三角域的 Bézier 曲面。为了方便运算和数据交换，研究它们之间的转换是有必要的。

三角域曲面 → 矩形域曲面

一个 $n$ 次三角域 Bézier 曲面（控制点 $T_{ijk}, i+j+k=n$）可以被精确地表示为一个 退化的 $n \times n$ 次矩形域 Bézier 曲面。

\[\left(\begin{array}{c} P_{i 0} \\ P_{i 1} \\ \vdots \\ P_{i n} \end{array}\right)=A_{1} A_{2} \ldots A_{i}\left(\begin{array}{c} T_{i 0} \\ T_{i 1} \\ \vdots \\ T_{i, n-i} \end{array}\right), \quad i=0,1, \cdots, n,\]

$A_i$ 是一个升阶算子：

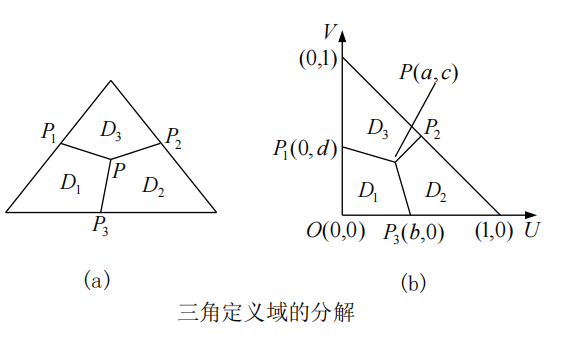
\[A_{k}=\left(\begin{array}{cccccc} 1 & 0 & 0 & \cdots & 0 & 0 \\ \frac{1}{n+1-k} & \frac{n-k}{n+1-k} & 0 & \cdots & 0 & 0 \\ 0 & \frac{2}{n+1-k} & \frac{n-k-1}{n+1-k} & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & \frac{n-k}{n+1-k} & \frac{1}{n+1-k} \\ 0 & 0 & 0 & \cdots & 0 & 1 \end{array}\right)_{(k+1) \times k}\]

另一种思路是将三角域曲面表示为 三个 非退化的矩形域 Bézier 曲面。这通常通过将三角域参数空间 $(u,v,w)$ 分割成三个子区域（例如，通过连接重心到边的中点），然后在每个子区域上定义一个矩形域曲面来实现。这需要进行参数变换和控制点计算。

一些算子（Operator）

• 单位算子： $I: I T_{i j}=T_{i j}$
• 移位算子： $E_{i}: E_{1} T_{i j}=T_{i+1, j}, E_{2} T_{i j}=T_{i, j+1}$
• 差分算子： $\Delta_{i}: \Delta_{1} T_{i j}=T_{i+1, j}-T_{i j}, \Delta_{2} T_{i j}=T_{i, j+1}-T_{i j}$

利用这些算子，我们可以将三角域Bézier曲面重写为：

\[\begin{aligned} T(u, v) & =\left(u E_{1}+v E_{2}+(1-u-v) I\right)^{n} T_{00} \\ & =\left(\Delta_{1} u+\Delta_{2} v+I\right)^{n} T_{00} \end{aligned}\]

定义在 $D_1$ 上的控制顶点可以通过下式获得：

\[\begin{array}{l} P_{i j}=\sum_{\substack{k=0 \\ k+l=j}}^{i} \sum_{\substack{i=0}}^{n-i}\binom{i}{k} \frac{\binom{n-i}{l}}{\binom{n}{j}} Q_{k l}^{(i)} \quad 0 \leqslant i, j \leqslant n,\\ \text { in which for } 0 \leqslant i \leqslant n, 0 \leqslant k \leqslant i, 0 \leqslant l \leqslant n-i \text {, }\\ Q_{k l}^{(i)}=\left(a E_{1}+c E_{2}+(1-a-c) I\right)^{k}\left(b E_{1}+(1-b) I\right)^{i-k}\left(d E_{2}+(1-d) I\right)^{l} T_{00} \end{array}\]

相关人物与概念：Christoph M. Hoffmann 与几何约束求解

在计算机辅助设计和几何造型领域，除了曲线曲面表示本身，几何约束求解 (Geometric Constraint Solving, GCS) 是另一个核心基础技术。它研究如何根据用户施加的几何约束（如距离、角度、平行、相切等）来确定几何对象的形状和位置。

Christoph M. Hoffmann 是普渡大学（Purdue University）的著名教授，在几何计算领域做出了杰出贡献。他发表了大量高影响力论文，H-Index 高。他的主要贡献包括：

• 几何计算的鲁棒性: 研究如何处理计算机浮点运算带来的误差，确保几何算法在实际应用中的稳定性和正确性。
• 几何约束求解: 开发了多种 GCS 理论和算法。

Hoffmann 曾在康奈尔大学与图灵奖得主 John Hopcroft 合作。Hopcroft 在算法设计领域有诸多贡献，包括与 Richard Karp 合作提出的二分图最大匹配的 $O(n^{5/2})$ 算法（SIAM J. Comput., 1973）。GCS 系统是现代 CAD 软件的基石，允许用户通过约束而非精确坐标来设计零件，极大地提高了设计效率和灵活性。Hoffmann 因其在 GCS 和鲁棒几何计算方面的贡献荣获 2011 年 Bézier 奖。

总结

Bézier 曲线和曲面以其优良的数学性质（如端点插值、凸包性、几何不变性）和直观的控制方式（通过控制点），成为了计算机辅助几何设计（CAGD）和计算机图形学中表示自由形态形状的基础工具。理解其定义、性质、求值算法（de Casteljau）、连续性条件以及度操作（升阶、降阶）对于深入学习和应用几何造型技术至关重要。从曲线到矩形域和三角域曲面，Bézier 方法提供了一套强大而灵活的建模手段。