光线跟踪加速技术详解

光线跟踪（Ray Tracing）作为计算机图形学领域的一项革命性技术，以其能够模拟光线的物理传播路径，生成具有高度真实感图像（包括精确的阴影、反射、折射、透明效果等）而闻名。自其诞生以来，光线跟踪一直是追求极致视觉效果的重要手段。然而，其逼真的效果往往伴随着巨大的计算开销。本文将深入探讨光线跟踪效率低下的原因，并详细介绍一系列用于加速光线跟踪的关键技术和数据结构。

回忆：光线跟踪的基本原理

光线跟踪的核心思想是从视点（摄像机）出发，为屏幕上的每个像素发射一条或多条光线，跟踪这些光线在场景中与物体的交互过程，根据交互结果计算像素的颜色。这是一个递归的过程，当光线与物体表面相交时，需要计算局部光照（考虑光源、材质属性），并可能产生新的反射光线和折射光线，继续递归地跟踪下去。

一个典型的递归光线跟踪算法可以表示为如下伪代码：

Color IntersectColor(Point vBeginPoint, Vector vDirection) {
    Color color = ambient_color; // Start with ambient light
    IntersectPoint intersectPoint = FindNearestIntersection(vBeginPoint, vDirection);

    if (intersectPoint exists) {
        // Calculate local shading (diffuse, specular) considering lights
        for each light_source {
            color += CalculateLocalShading(intersectPoint, normal, light_source);
        }

        SurfaceProperties surface = GetSurfaceProperties(intersectPoint);

        // Handle reflection
        if (surface.isReflective) {
            Vector reflectRayDirection = CalculateReflectionDirection(vDirection, normal);
            color += surface.reflectCoefficient *
                     IntersectColor(intersectPoint, reflectRayDirection);
        }
        // Handle refraction
        else if (surface.isRefractive) {
            Vector refractRayDirection = CalculateRefractionDirection(vDirection, normal, surface.refractiveIndex);
            color += surface.refractCoefficient *
                     IntersectColor(intersectPoint, refractRayDirection);
        }
    } else {
        // No intersection, return background color or default
        color = background_color;
    }

    return color;
}

图：光线跟踪技术能够生成包含复杂光学现象的真实感图像

光线跟踪加速：动机

尽管光线跟踪效果出众，但其计算效率往往成为瓶颈。主要原因在于：

1. 高时间复杂度：对于包含大量物体的复杂场景，每条光线可能需要与场景中的许多物体进行相交测试。最朴素的实现中，时间复杂度与场景复杂度（如三角面片数量）成正比。
2. 高空间复杂度：存储场景几何信息和可能的加速结构本身就需要大量内存。
3. 几何运算密集：算法的大部分时间消耗在可见性判断（光线与哪个物体首先相交）和求交测试（计算精确交点）这些几何运算上。

因此，研究和应用光线跟踪加速技术对于使其在交互式应用（如游戏）和大规模场景渲染中变得可行至关重要。

光线跟踪加速方案

加速光线跟踪的核心思想是尽量减少不必要的、昂贵的光线-物体相交测试次数。这通常通过构建和利用空间数据结构（Spatial Data Structures）来实现。这些结构能够有效地组织场景中的几何体，使得光线可以快速地确定可能与之相交的物体子集。常见的空间数据结构包括：

• 层次包围体 (Bounding Volume Hierarchies, BVH)
• 均匀格点 (Uniform Grids)
• 四叉树/八叉树 (Quadtree/Octree)
• 空间二分树 (K-d tree/BSP tree)

使用合适的空间数据结构，可以将光线跟踪算法的性能提升 10 到 100 倍，甚至更多。

光线求交基础

在讨论加速结构之前，我们先回顾一下光线求交的基本问题：给定一个模型（通常由大量三角面片组成）和一条光线（由起点 $P_0$ 和方向向量 $\vec{d}$ 定义），如何快速判定光线是否与模型相交？如果相交，如何快速求出第一个交点的坐标？

最简单直接的方法是遍历模型中的每一个三角面片，并进行光线-三角形相交测试：

boolean IsIntersect(Ray r, Model m) {
    for each triangle t in m {
        if (IsIntersect(t, r)) {
            return true; // Found an intersection
        }
    }
    return false; // No intersection found
}

这种方法的缺点显而易见：其时间复杂度为 $O(n)$，其中 $n$ 是模型包含的三角面片数量。对于复杂模型，这会非常耗时。

包围体 (Bounding Volumes, BV)

包围体技术是加速求交测试的一种基本而有效的方法。其思想是：用一个几何形状简单（易于进行光线相交测试）的物体将复杂的物体或一组物体包裹起来。这个简单的几何体就是所谓的包围体。

常见的包围体类型有：

1. 长方体包围盒 (Bounding Box)：可以是轴对齐包围盒 (Axis-Aligned Bounding Box, AABB)，其各面平行于坐标轴；也可以是有向包围盒 (Oriented Bounding Box, OBB)，其方向可以任意。
2. 包围球 (Bounding Sphere)。

包围体的应用逻辑如下： 在进行光线与复杂物体的精确相交测试之前，先进行光线与该物体包围体的相交测试。

• Easy Reject：如果光线与包围体不相交，那么它一定不会与内部的物体相交，可以直接排除，避免了昂贵的精确求交测试。
• 如果光线与包围体相交，则需要进一步进行光线与物体的精确相交测试。

轴对齐包围盒 (AABB)

AABB 的构造非常简单。只需遍历物体的所有顶点，找到 $x, y, z$ 坐标的最小值和最大值：$(x_{min}, x_{max}), (y_{min}, y_{max}), (z_{min}, z_{max})$。这个由 $[x_{min}, x_{max}] \times [y_{min}, y_{max}] \times [z_{min}, z_{max}]$ 定义的长方体就是该物体的 AABB。构造时间复杂度为 $O(N)$，其中 $N$ 是顶点数量。AABB 的光线求交测试也相对高效。

有向包围盒 (OBB) 与 Kay-Kajiya 方法

虽然 AABB 易于构建和测试，但其轴对齐的特性可能导致包围不够紧密，特别是对于斜向放置的细长物体。OBB 可以更紧密地贴合物体的形状，从而提供更好的剔除效率。

构建最优 OBB 是一个较复杂的问题，通常需要使用迭代算法。

Kay 和 Kajiya 在 1986 年提出了一种构建更紧密包围盒的方法（虽然原文是针对层次包围盒，但其思想也适用于单个物体的包围）。他们指出，仅使用轴对齐平面可能不够紧密。他们建议根据景物的实际形状，选取 $n$ 组不同方向的平行平面来包裹物体。一个平面可以由方程 $Ax + By + Cz - d = 0$ 定义。假设法向量 $\vec{N} = (A, B, C)$ 是单位向量，则 $d$ 表示平面到原点的距离。对于给定的法向量 $\vec{N}_i$，总存在一个 $d_i^{near}$ 和 $d_i^{far}$，使得由这两个平面定义的平板（slab）刚好包裹住物体。通过几组（Kay 和 Kajiya 建议 $n < 5$）这样的平板相交，可以形成一个比 AABB 更紧密的凸体包围盒。

图：使用多个方向的平面（平板）相交可以形成更紧密的包围体

如何确定 $d_i^{near}$ 和 $d_i^{far}$？

• 对于多面体模型：可以将所有顶点投影到法线方向 $\vec{N}_i$ 上，计算投影距离（即点到原点沿 $\vec{N}_i$ 方向的距离 $A x + B y + C z$）的最小值和最大值，即为 $d_i^{near}$ 和 $d_i^{far}$。
• 对于隐式曲面 $F(x, y, z) = 0$：需要找到函数 $f(x, y, z) = Ax + By + Cz$ 在约束条件 $F(x, y, z) = 0$ 下的极大值和极小值。这通常可以使用 Lagrange 乘子法 来求解。

包围球 (Bounding Sphere)

包围球由球心和半径定义。它的一个优点是旋转不变性：当物体旋转时，其包围球只需平移，半径和形状不变。光线-球体相交测试也非常简单高效。

计算一个点集的最小包围球（Minimum Bounding Sphere）是一个经典的计算几何问题。存在精确算法，但复杂度较高。一个常用的近似算法具有 $O(N)$ 时间复杂度（$N$ 为点数），生成的包围球通常只比最优解大 5% 左右。该近似算法步骤如下：

1. 初始化：遍历所有点，找到 $x, y, z$ 坐标分别最小和最大的点。计算这三对点（$x_{min}/x_{max}$ 点对, $y_{min}/y_{max}$ 点对, $z_{min}/z_{max}$ 点对）之间的距离。选择距离最大的一对点，以连接它们的线段作为初始包围球的直径。
2. 迭代调整：再次遍历所有点。如果发现某个点 $P$ 位于当前包围球 $S$ 的外部，则需要调整包围球。创建一个新的包围球 $S’$，它刚好包含原来的球 $S$（内切）并且也包含点 $P$。这个新的球 $S’$ 成为当前的包围球。
3. 重复步骤 2 直到所有点都包含在内，或者迭代一定次数。

包围体的应用与求交

包围体不仅用于光线跟踪加速，还在隐藏面消除、碰撞检测等图形学领域有广泛应用。光线与 AABB 和包围球的求交计算相对简单，是图形学中的基础内容（通常在介绍光线跟踪基础时讲解）。

层次包围体 (Bounding Volume Hierarchy, BVH)

单个包围体虽然能有效剔除与单个物体的相交测试，但如果场景中有 $n$ 个物体，每个物体都有一个包围体，那么光线仍然需要与 $n$ 个包围体进行测试，时间复杂度仍为 $O(n)$。

为了进一步提高效率，可以引入层次结构。层次包围体 (BVH) 就是一种基于包围体的树状结构。

• 结构：BVH 树的叶子节点通常对应场景中的一个或少数几个基本图元（如三角形），并包含这些图元的紧密包围体。每个内部节点则包含一个包围体，该包围体是其所有子节点包围体的并集（通常是包围这些子包围体的最小包围体）。
• 构建：BVH 通常采用自顶向下或自底向上的方式构建。自顶向下方法从包含整个场景的根节点开始，递归地将节点中的物体集划分到两个或多个子节点中，并为每个子节点计算新的包围体，直到满足终止条件（如节点中物体数量小于阈值或达到最大深度）。自底向上方法从每个物体的包围体（叶节点）开始，逐步合并相近的节点形成父节点，直至形成单一的根节点。
• 遍历：利用 BVH 进行光线求交时，从根节点开始：
  1. 测试光线是否与当前节点的包围体相交。
  2. 如果不相交，则该节点及其所有子孙节点代表的物体都无需再考虑（剪枝），直接返回。
  3. 如果相交：
     • 若当前节点是叶节点，则测试光线与该叶节点包含的所有图元，记录最近的交点。
     • 若当前节点是内部节点，则递归地对其子节点进行遍历。通常会优先遍历距离光线起点更近的子节点。

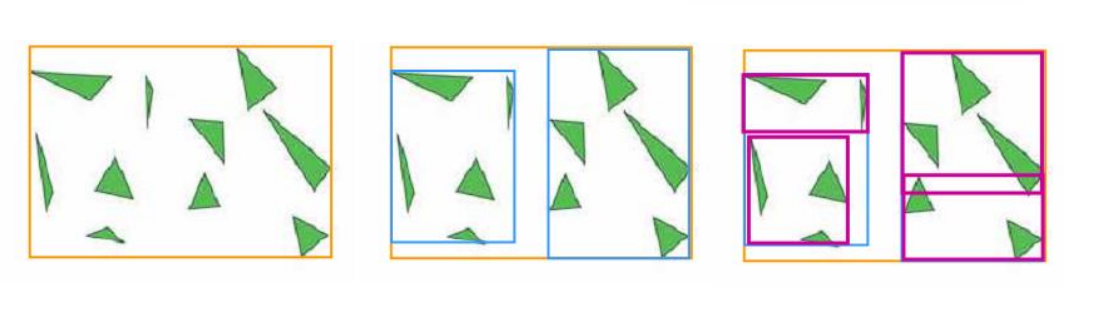图：一个2D场景及其对应的BVH树结构 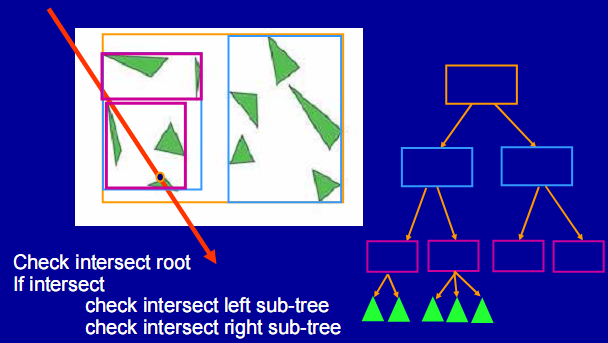图：利用BVH进行光线求交的过程，光线仅需测试与根节点及其相交子节点包围体，以及最终叶节点内的图元

一个有趣的性质是，BVH 中不同子节点的包围体可能会相互重叠。

BVH 的主要优点在于其高效的剪枝能力。对于分布良好的场景和构建良好的 BVH，光线遍历的平均时间复杂度可以从 $O(n)$ 降低到 $O(\log n)$。此外，BVH 非常灵活，可以在不同层级或针对不同类型的几何体使用不同类型的包围体（如 AABB, OBB, Sphere）。

空间划分 (Spatial Partitioning)

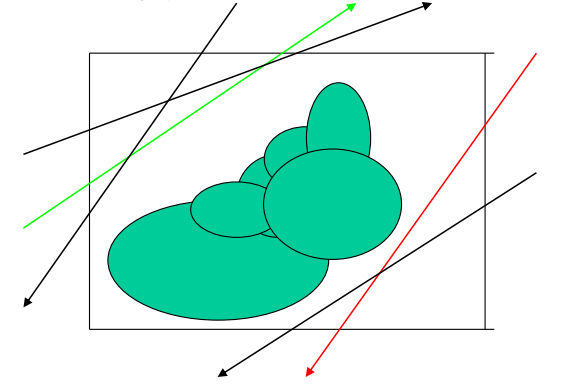
除了基于物体组织（如 BVH）的加速结构外，另一大类方法是空间划分，即将场景空间本身划分为多个区域（通常称为单元或体素），并记录每个区域中包含哪些物体。光线在空间中传播时，只需与其穿过的区域内的物体进行相交测试。

均匀格点 (Uniform Grids)

这是最简单的空间划分方法。将包含整个场景的包围盒划分为一个三维的、由相同大小立方体单元（格点）组成的阵列。

• 预处理：对于每个格点单元，存储一个列表，包含所有与该单元相交的物体（或物体的一部分，如三角形）。
• 遍历：光线跟踪时，首先确定光线起点所在的格点单元。然后，沿着光线的路径，步进式地确定光线依次穿过的格点单元。对于光线穿过的每个单元，测试光线与该单元关联列表中的所有物体。记录遇到的第一个交点。如果光线穿出整个格点区域仍未找到交点，则认为光线未与场景相交。

确定光线穿过的下一个格点单元可以使用一种类似于数字微分分析器 (DDA) 的算法。其基本思想是计算光线穿过当前单元到达下一个 $x, y, z$ 方向格点边界所需的参数 $t$ 值（$t_{next_x}, t_{next_y}, t_{next_z}$），选择其中最小的一个，更新当前单元索引，并更新该方向的 $t$ 值。

在 3D 情况下，假设光线方向为 $(dir_x, dir_y, dir_z)$，格点尺寸在各轴上分别为 $grid_x, grid_y, grid_z$。则光线在 $x, y, z$ 方向上穿过一个单元所需增加的参数 $t$ 分别为 $\Delta t_x = \frac{grid_x}{|dir_x|}, \Delta t_y = \frac{grid_y}{|dir_y|}, \Delta t_z = \frac{grid_z}{|dir_z|}$。 当前单元为 $(i, j, k)$，下一个可能穿过的单元边界对应的参数值为 $t_{next_x}, t_{next_y}, t_{next_z}$。

// Simplified 3D DDA logic for grid traversal
// Assuming initialization of i, j, k, t_next_x, t_next_y, t_next_z
// and calculation of stepX, stepY, stepZ (+1 or -1 based on ray direction)
// and dtx, dty, dtz (delta t values)

while (within grid bounds) {
    if (t_next_x < t_next_y && t_next_x < t_next_z) {
        current_t = t_next_x;
        i += stepX;
        t_next_x += dtx;
    } else if (t_next_y < t_next_z) {
        current_t = t_next_y;
        j += stepY;
        t_next_y += dty;
    } else {
        current_t = t_next_z;
        k += stepZ;
        t_next_z += dtz;
    }

    // Process cell (i, j, k) - check intersections with objects in this cell
    if (IntersectWithObjectsInCell(i, j, k, ray, current_t)) {
         return nearest_intersection;
    }
}

这个过程与直线光栅化算法有相似之处。

优点：均匀格点结构简单，易于构建和遍历。 缺点：对场景中物体分布的非均匀性非常敏感。如果场景中的物体集中在少数区域（例如 “体育场中的茶壶” 问题），那么大部分格点单元可能是空的，导致光线需要遍历大量空单元；而少数包含大量物体的单元则可能成为新的瓶颈。此外，选择合适的格点分辨率是一个难题：太少，每个单元物体过多；太多，内存消耗大且空单元遍历开销大。

四叉树/八叉树 (Quadtree/Octree)

为了克服均匀格点对非均匀分布的敏感性，可以使用自适应的空间划分结构，如四叉树（2D）和八叉树（3D）。

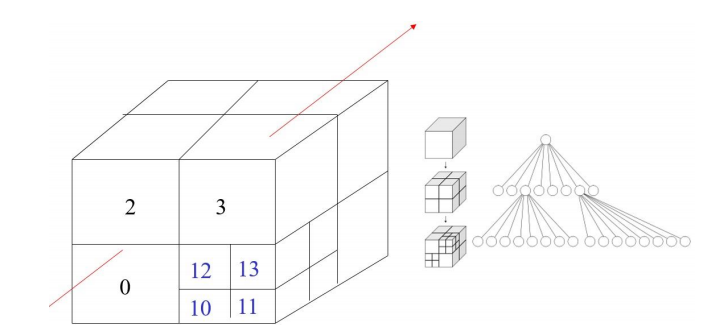
• 八叉树 (Octree)：从一个包含整个场景的立方体（根节点）开始，递归地将其划分为 8 个等大的子立方体（子节点）。如果一个节点对应的立方体足够 “简单”（例如，包含的物体数量少于阈值，或达到预设的最大深度），则停止划分，该节点成为叶节点。否则，继续对其进行八分。
• 构建：通常采用自顶向下递归构建。物体（如图元）通常存储在包含它们的叶节点中。一个跨越多个子立方体边界的物体可能会被存储在多个叶节点中，或者需要特殊处理（如切割，或存储在能够完全包含它的最小层级的节点上）。
• Octree-R：标准八叉树的划分平面固定在父立方体的中心。Octree-R 是一种变体，允许划分平面更自由地选择位置（通常基于某种启发式策略），目的是减少物体跨越多个单元的情况，从而提高效率。研究表明，Octree-R 相较于标准 Octree 可能带来 4%-47% 的性能提升，具体取决于场景。
• 子节点寻址：
  • 指针：每个内部节点存储 8 个指向其子节点的指针。
  • 编码：可以使用一种基于路径的编码方案。例如，如果根节点编码为空，其子节点可以编码为 0 到 7。下一层级的子节点编码则在其父节点编码后追加 0 到 7。这种方式便于计算和存储。 图：八叉树子节点的一种编码方式 (0-7)

八叉树空间剖分细节：

假设空间被归一化到一个单位立方体，八叉树深度为 $N$。

• 节点编码：一个深度为 $i$ 的节点可以编码为 $q_1 q_2 \cdots q_i FF \cdots F$（$N-i$ 个 F），其中 $q_k \in {0, 1, \dots, 7}$。$F$ 可视为一个特殊标记。
• 定位点：空间中一点 $P(x, y, z)$（坐标归一化并视为 $N$ 位二进制整数 $x = i_1 i_2 \cdots i_N$, $y = j_1 j_2 \cdots j_N$, $z = k_1 k_2 \cdots k_N$）所在的最底层（深度 N）单元格的编码为 $q_1 q_2 \cdots q_N$，其中 $q_l = i_l + 2j_l + 4k_l$ ($l = 1, \dots, N$)。这个性质允许快速定位点所在的最小单元。
• 节点范围：给定一个编码为 $q_1 q_2 \cdots q_i FF \cdots F$ 的节点，其对应的空间立方体范围（前左下角坐标）可以通过 $q_1 \dots q_i$ 推算出来（本质上是根据每层编码确定坐标范围）。

光线在八叉树中的遍历：

1. 起点定位：确定光线起点 $P_0$ 所在的最小单元格编码 $Q = q_1 q_2 \cdots q_N$ (使用性质1)。处理边界情况。
2. 树中查找：在八叉树中查找与编码 $Q$ 匹配最深的叶节点。设找到的叶节点编码为 $Q’ = q_1 q_2 \cdots q_i FF \cdots F$ (匹配 $i$ 位)。
3. 求交测试：如果找到了叶节点 ($T$=true)，则测试光线与该叶节点关联的所有物体。若有交点，返回最近交点。若无交点，或当前节点不是叶节点/是空叶节点 ($T$=false)，则需前进到下一个单元。
4. 步进：计算光线离开当前单元（由 $Q’$ 定义）的出口点。这个出口点成为新的起点 $P_0$。更新 $P_0$ 所在的新单元编码 $Q$，回到步骤 2。可以使用类似于 3D DDA 的方法高效计算出口点和下一个单元。

八叉树遍历的复杂性：光线在八叉树中的遍历通常比在均匀格点中更复杂，因为需要递归下降和上升，并且光线可能与一个内部节点的多个子节点相交，需要确定正确的访问顺序。

空间二分树 (BSP Tree / K-d Tree)

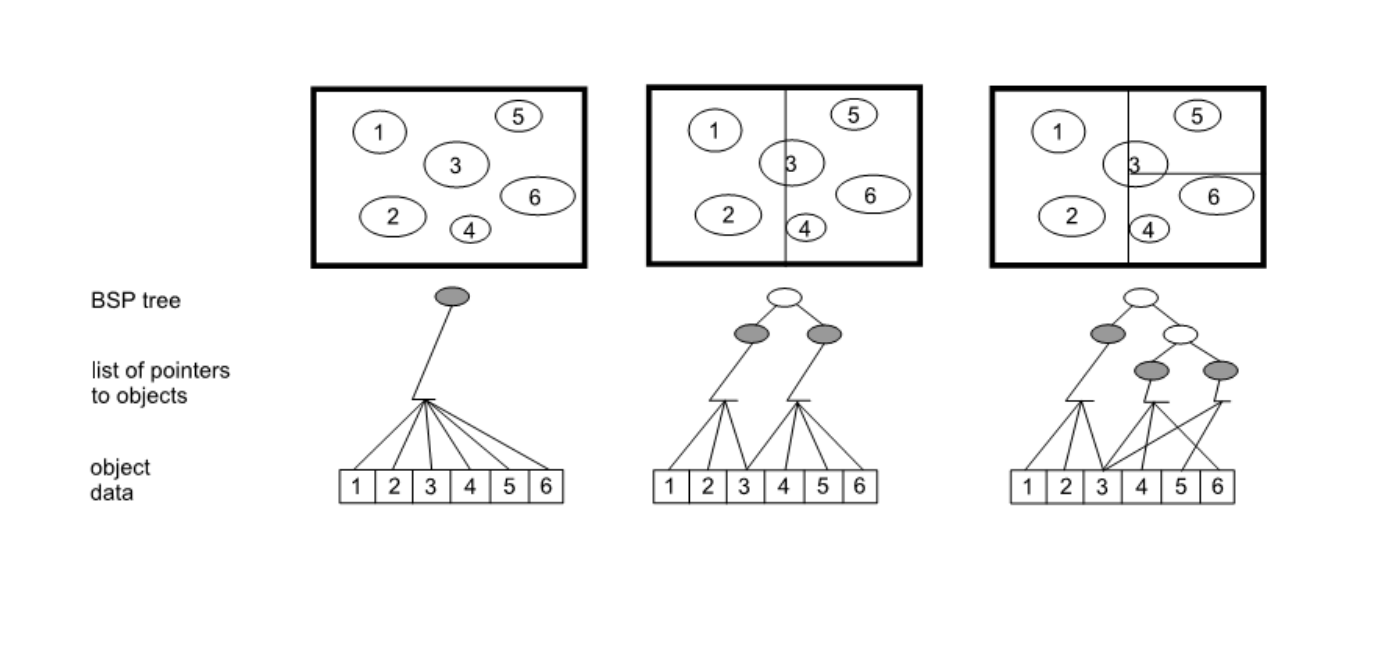
BSP 树 (Binary Space Partitioning Tree) 是一种递归地使用超平面（在 3D 中是平面）将空间划分为两个子空间的结构。

• 类型：
  • Polygon-aligned BSP Tree：使用场景中多边形所在的平面作为划分平面。主要用于完全由多边形构成的场景，可以用于隐藏面消除。
  • Axis-aligned BSP Tree：划分平面总是平行于某个坐标轴（$x=c, y=c,$ 或 $z=c$）。
• 构建 (Axis-aligned)：类似于八叉树，采用自顶向下递归构建。每次选择一个轴（通常按 $x, y, z$ 轮换）和一个位置，用一个垂直于该轴的平面将当前节点的空间区域划分为两个子区域，分别对应左右子节点。
  • BSP vs K-d Tree：一个关键区别在于划分平面的位置。严格的 BSP 树（某些定义下）要求划分平面位于区域的中点，将空间等分为二。而 K-d 树 (k-dimensional tree) 则更灵活，划分平面的位置可以任意选择（通常选择中位数位置或其他启发式位置，以更好地平衡树或隔离物体）。因此，轴对齐 BSP 树可以看作是 K-d 树的一种特例。
• 优点：轴对齐划分使得光线与划分平面的求交计算非常简单高效（只需比较一个坐标）。
• 缺点：由于划分位置的限制（特别是严格中点划分的 BSP），物体可能会被划分平面切割，需要特殊处理（如将物体分配到两个子节点，或分割物体）。K-d 树通过灵活选择划分位置，可以一定程度上缓解这个问题。

图：一个2D空间的轴对齐BSP/K-d树划分示例

光线在 BSP/K-d 树中的遍历：

遍历过程通常是递归的。一个典型的（K-d 树）遍历函数如下：

// Pseudo-code for Ray Traversal in a K-d Tree (similar to BSP)
void RayTreeIntersect(Node node, Ray ray, float t_min, float t_max) {
    if (node is Leaf) {
        // Intersect ray with objects in the leaf node
        // Update nearest intersection found so far if intersection occurs within [t_min, t_max]
        IntersectWithObjectsInLeaf(node, ray, t_min, t_max);
        return;
    }

    // Node is internal
    Axis axis = node.splitAxis; // x, y, or z
    float splitPos = node.splitPosition;
    int nearChildIndex, farChildIndex;

    // Determine which child is nearer to the ray origin along the split axis
    if (ray.origin[axis] < splitPos || (ray.origin[axis] == splitPos && ray.direction[axis] <= 0)) {
        nearChild = node.leftChild;
        farChild = node.rightChild;
    } else {
        nearChild = node.rightChild;
        farChild = node.leftChild;
    }

    // Calculate intersection distance 't_split' with the splitting plane
    float t_split;
    if (ray.direction[axis] == 0) { // Ray parallel to plane
        t_split = infinity; // Or handle appropriately
    } else {
        t_split = (splitPos - ray.origin[axis]) / ray.direction[axis];
    }

    // Recursively traverse children based on t_split relative to [t_min, t_max]
    if (t_split > t_max || t_split <= 0) { // Split plane is beyond far extent or behind origin
        RayTreeIntersect(nearChild, ray, t_min, t_max);
    } else if (t_split < t_min) { // Split plane is before near extent
        RayTreeIntersect(farChild, ray, t_min, t_max);
    } else { // Split plane is within [t_min, t_max], ray crosses plane
        // Traverse near child first, within [t_min, t_split]
        RayTreeIntersect(nearChild, ray, t_min, t_split);
        // Then traverse far child, within [t_split, t_max], only if needed
        // (Check if nearest intersection found so far is > t_split)
        if (nearest_hit_t > t_split) {
             RayTreeIntersect(farChild, ray, t_split, t_max);
        }
    }
}

// Initial call:
// RayTreeIntersect(rootNode, ray, t_entry, t_exit);
// where t_entry and t_exit are intersection distances with the root bounding box

此伪代码展示了 K-d 树的递归遍历逻辑。它计算光线与划分平面的交点参数 t_split，并根据 t_split 相对于当前光线段有效范围 [t_min, t_max] 的位置，决定是只遍历近子节点、只遍历远子节点，还是先遍历近子节点再（可能）遍历远子节点。这种顺序保证了找到的是光线路径上的第一个交点。通过维护一个栈可以将其转化为迭代形式，减少函数调用开销。

研究表明，光线在 K-d 树（或优化的 BSP 树）中的遍历通常比在八叉树中快约 10%。

其他光线跟踪相关技术

除了上述核心的加速结构外，还有一些改进的光线跟踪算法和相关技术。

分布式光线跟踪 (Distributed Ray Tracing)

也称为随机光线跟踪 (Stochastic Ray Tracing)，由 Cook, Porter 和 Carpenter 提出。它通过在光线跟踪过程中引入随机采样来模拟传统光线跟踪难以实现的软效果 (Soft Phenomena)。

传统光线跟踪通常：

• 为每个像素中心发射一条主光线（导致锯齿，Aliasing）。
• 从交点向每个点光源发射一条阴影光线（导致硬阴影，Sharp Shadows）。
• 只产生一个理想的反射和折射方向（导致完美镜面反射/折射）。

分布式光线跟踪则通过在以下维度上进行分布采样（发射多条随机扰动的光线）来克服这些限制：

• 像素区域：在像素覆盖的区域内发射多条光线并平均结果，实现反走样 (Anti-aliasing)。
• 光源面积：将点光源视为面光源，向光源表面上的多个点发射阴影光线，模拟软阴影 (Soft Shadows)。 图：点光源（硬阴影）与面光源（软阴影）效果对比
• 反射/折射方向：根据材质的 BRDF/BTDF，在理想反射/折射方向周围采样多个方向，实现模糊反射/折射 (Glossy Reflections/Refractions)。 图：模糊（光泽）反射效果
• 透镜孔径：模拟相机的有限光圈，从透镜上的不同点发射光线，实现景深 (Depth of Field, DoF) 效果。 图：景深效果，焦点外物体模糊
• 时间：在快门开启的时间段内对光线发射时间进行采样，模拟运动模糊 (Motion Blur)。 图：运动模糊效果

分布式光线跟踪极大地扩展了光线跟踪能够模拟的物理现象范围，但代价是需要发射更多的光线，计算量更大。

光束跟踪 (Beam Tracing)

由 Heckbert 和 Hanrahan 在 1984 年提出，是光线跟踪的一个变种，旨在利用光线之间的空间相干性。它跟踪的不是无限细的射线，而是具有一定截面形状的光束（通常是锥形或多边形截面的棱柱/棱锥）。

• 过程：从视点出发，初始光束覆盖整个视场（或屏幕的一个区域）。当光束与场景中的多边形相交时，会被部分遮挡、反射或折射，产生新的、形状可能更复杂的光束。这个过程可以组织成一棵光束树。
• 场景：原始的光束跟踪主要针对多边形场景。
• 变换：为了方便处理，通常会将场景变换到光束的局部坐标系中。例如，对于反射，可以使用一个反射变换矩阵 $M_r$ 将场景物体变换到反射光束看起来像是从虚像位置发出（即入射光束的延伸）的坐标系中。
  • 反射变换：点 $P_r$（反射光线上）与其虚像点 $P$ 的关系为 $P = P_r - 2 (L \cdot P_r) \vec{N} = M_r P_r$，其中 $L$ 是平面方程参数，$ \vec{N}$ 是单位法向量。$M_r$ 是一个 4x4 齐次变换矩阵。
• 求交：在变换后的坐标系中，光束通常是轴向的（如柱体）。求交过程变为：将场景中的多边形也进行相应变换，并按深度排序。然后，在光束的横截面（如 xy 平面）上，将光束的截面多边形与场景多边形的投影进行二维布尔运算（求交、求差），以确定光束被哪些多边形以及如何遮挡。
• 折射：折射变换是非线性的。Heckbert 等人提出了一种近似线性变换 $M_t$，假设光线接近垂直入射且折射率恒定。$P = P_t + \alpha (L \cdot P_t) \vec{M} = M_t P_t$，其中 $\alpha$ 与折射率相关，$\vec{M}$ 是与法线和入射方向相关的向量。
• 着色：最终像素颜色通过遍历光束树，组合所有可见表面片段（fragments）的光照贡献来计算。公式类似于光线跟踪：$I = C_d I_d + C_s I_s + \sum C_r I_r + \sum C_t I_t$，其中 $I_r, I_t$ 是通过递归遍历子光束计算得到的整体反射和折射光亮度。

光束跟踪在处理某些特定场景（如室内、多边形为主）时可能比光线跟踪更高效，因为它一次处理一批相关的光线。

其他优化技术

• 选择性光线跟踪与插值：并非对每个像素都进行完整的光线跟踪。可以选择性地只对某些“关键”像素（如物体边缘、高频区域）进行跟踪，然后对其余像素的颜色进行插值。如何智能地选择这些关键像素是该技术的重点。
• 基于小波 (Wavelet) 的重要性采样：利用小波变换来分析图像或场景的频率特性，指导重要性采样 (Importance Sampling)，即优先在变化剧烈或贡献大的区域投入更多计算资源（如发射更多光线）。
• ReSTIR (Reservoir Spatio-Temporal Importance Resampling)：SIGGRAPH 2020 提出的一种先进的实时渲染技术，用于高效地渲染大量光源（如百万级）的直接光照。它利用蓄水池采样 (Reservoir Sampling) 结合时空复用思想：在空间上，复用相邻像素的采样信息；在时间上，复用前一帧中对应场景点的采样信息，极大地提高了采样效率。

硬件加速

随着光线跟踪的重要性日益增加，专用硬件加速也成为了研究和发展的热点。例如，RPU (Ray Processing Unit) 项目（SIGGRAPH 2005）探索了用于实时光线跟踪的可编程硬件单元，能够对材质、几何和光照进行编程。如今，现代 GPU 中集成的 RT Core 就是光线跟踪硬件加速的商业化成果。

今日人物：Thomas W. Sederberg

• Thomas W. Sederberg： Brigham Young University (BYU) 教授。
• 背景： BYU 土木工程学士、硕士，普渡大学机械工程博士。自 1983 年起在 BYU 任教。
• 贡献：发表论文 140 余篇，被引次数超过 18742 次 (H-Index: 54)。在计算机图形学和几何建模领域做出杰出贡献，包括：
  • 自由形式变形 (Free-Form Deformation, FFD)：SIGGRAPH 论文被引超过 4500 次。
  • 形状混合/变形 (Shape Blending)。
  • T-样条 (T-Splines) 和非均匀有理细分曲面 (NURSS)：被引超过 1370 次，对 CAD/CAM 领域影响深远。
• 荣誉：
  • 2006 年 ACM SIGGRAPH Computer Graphics Achievement Award。
  • 2013 年 Solid Modeling Association 的 Pierre Bézier Award。

Sederberg 教授的工作极大地推动了计算机辅助几何设计和图形学的发展。

总结

光线跟踪因其无与伦比的真实感效果而备受青睐，但其固有的高计算复杂度是实际应用中的主要障碍。本文探讨了加速光线跟踪的强烈动机，并详细介绍了一系列关键的加速技术，核心在于利用空间数据结构（如 BVH, 均匀格点, 八叉树, K-d/BSP 树）来有效减少昂贵的光线-物体相交测试次数。此外，还讨论了分布式光线跟踪、光束跟踪以及其他优化方法，它们进一步扩展了光线跟踪的能力和效率。随着算法的不断进步和硬件加速的发展，光线跟踪正越来越多地从离线渲染走向实时应用。