光线跟踪算法基础
本文详细介绍光线跟踪算法的基本原理、历史发展与实现方法,包括光线与场景求交、光线投射、Whitted-Style光线跟踪和蒙特卡洛路径追踪等技术,以及与传统光栅化渲染的区别与应用场景。
计算机图形学致力于在计算机中创建、存储和操纵几何模型以及生成这些模型的图像。真实感绘制是其核心目标之一,旨在生成与真实世界照片难以区分的图像。在众多渲染技术中,光线跟踪 (Ray Tracing) 以其模拟物理光线传播的能力而闻名,能够产生高度逼真的视觉效果。本文将深入探讨光线跟踪的基础知识,包括其核心概念、关键算法以及实现中的挑战。
光线跟踪概述 (Ray Tracing Overview)
什么是光线跟踪?
光线跟踪是一种强大且被广泛使用的真实感绘制算法。与传统的光栅化技术主要处理局部光照不同,光线跟踪通过模拟光线在场景中的传播、反射和折射路径,能够有效地处理全局光照效果,例如光线的多次弹射,从而生成更加逼真的阴影、精确的反射和折射。因此,它有时也被称为“光线追踪”。
我们为何能看见物体?
从物理角度看,我们能看见物体是因为光线。光可以被理解为一系列由光源(如太阳、灯泡)发出,并在物体表面反复弹射的光线 (Rays)。当一部分经历了复杂路径的光线最终进入我们的视点(眼睛)时,我们便感知到了物体的存在、形状和颜色。
光线跟踪的核心思想正是模拟这一过程,但通常采用逆向路径:从视点(或虚拟相机)出发,经过屏幕上的每个像素,向场景中投射光线,追踪这些光线与物体的交互,最终确定像素的颜色。
光线跟踪的特征
光线跟踪算法的主要优势在于其物理直观性,这使得它能够相对容易地模拟出引人入胜的视觉效果:
- 精确的阴影 (Shadows): 通过追踪从表面点到光源的光线(阴影光线)是否被遮挡来判断。
- 镜面反射 (Reflection): 模拟光线在光滑表面的反射现象。
- 透明折射 (Refraction): 模拟光线穿过透明或半透明介质(如玻璃、水)时的路径弯曲。
此外,光线跟踪不仅适用于基本的几何形体(如球体、立方体),也同样适用于更复杂的物体表示方法,例如由大量三角形组成的多边形网格 (Polygon Mesh) 或通过布尔运算组合的复合形体 (Constructive Solid Geometry, CSG)。
历史地位与应用
光线跟踪的概念由来已久,但现代光线跟踪算法的里程碑式工作由 Turner Whitted 在 1980 年完成。他在其著名论文 “An improved illumination model for shaded display” (发表于 Communications of the ACM, Vol. 23, No. 6, pp. 343-349, June 1980, 最初展示于 SIGGRAPH 1979) 中,首次提出了一个包含精确反射和折射效果的光照模型(Whitted 模型),并给出了递归式光线跟踪算法 (Whitted-Style Ray Tracing) 的范例。这项工作极大地推动了真实感图形学的发展。
关于 Turner Whitted: Turner Whitted 于 1978 年在北卡罗来纳州立大学 (NCSU) 获得博士学位,随后加入贝尔实验室,在那里提出了他著名的光线跟踪算法。尽管他的学术生涯中发表的论文数量相对不多(约 36 篇,其中包含 11 篇 SIGGRAPH 和 2 篇 Communications of the ACM),但其影响力巨大。他于 2003 年当选为美国国家工程院院士。
早期的光线跟踪算法主要应用于可以精确建模的室内规则场景,例如著名的 康奈尔盒 (Cornell Box),它至今仍是测试和比较全局光照算法的标准场景之一。由于光线跟踪能够模拟复杂的光线传输,其渲染结果常被视为 “ground truth” (基准真相),用于验证和比较其他(通常是更快的)绘制方法的准确性。
光线跟踪 V.S. 光栅化
在讨论光线跟踪时,必然会与另一种主流渲染技术——光栅化 (Rasterization) 进行比较:
- 光栅化 (Rasterization):
- 优势: 速度快,拥有成熟的硬件加速渲染流水线(GPU),非常适合实时应用(如需要 >30 FPS 的电子游戏)。
- 劣势: 主要处理局部光照,模拟光线的多次弹射(全局光照效果,如软阴影、间接光照、精确反射折射)比较困难,通常需要依赖各种近似技巧 (hacks)。质量相对较低。
- 光线跟踪 (Ray Tracing):
- 优势: 能够基于物理原理模拟光线传播,渲染质量高,可以自然地产生各种全局光照效果,更接近真实物理世界。
- 劣势: 计算量巨大,传统上速度很慢,主要用于离线渲染(如电影特效、建筑可视化)。近年来,随着专用硬件(如 NVIDIA RTX 系列显卡)的发展,实时光线跟踪逐渐成为可能,并开始应用于游戏中。
光线求交 (Ray Intersection)
光线跟踪算法的核心计算瓶颈在于确定光线与场景中物体的可见交点(即光线求交)。对于场景中的每一条光线,都需要判断它首先与哪个物体相交,以及交点的位置。因此,高效且精确的光线-物体求交测试至关重要。
光线的表示
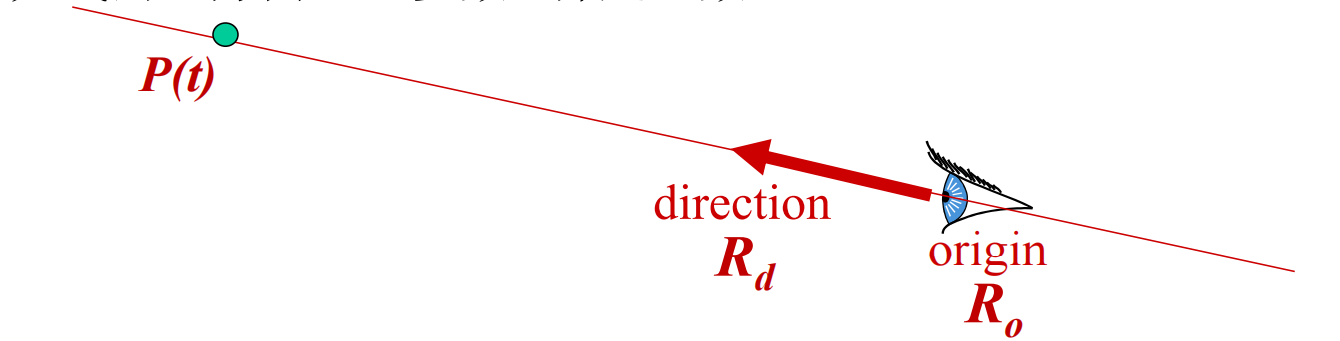
在三维空间中,一条光线(或射线)通常使用参数方程表示:
\[P(t) = R_o + t R_d\]其中:
- $R_o = (x_o, y_o, z_o)$ 是光线的 源点 (Origin)。
- $R_d = (x_d, y_d, z_d)$ 是光线的 方向向量 (Direction),通常被规范化为单位向量 (即 $|R_d| = 1$)。
- 参数 $t$ 是一个标量,表示沿光线方向的距离。对于光线(从源点出发的半无限直线),我们通常只关心 $t > 0$ 的部分,$P(t)$ 代表了光线上距离源点 $t$ 个单位长度的点。
光线与基本几何体的求交
下面我们讨论光线与几种常见几何图元求交的方法。
光线与平面 (Plane) 求交
平面是三维空间中最简单的表面之一。
- 平面的表示:
- 显式表示: 由平面上的一个点 $P_o = (x_o, y_o, z_o)$ 和平面的法向量 $n = (A, B, C)$ 定义。
- 隐式表示: 平面上的所有点 $P = (x, y, z)$ 都满足方程 $H(P) = Ax + By + Cz + D = 0$,或者写成向量形式 $n \cdot P + D = 0$。
- 点到平面的距离: 如果法向量 $n$ 是单位向量,那么任意点 $P$ 到平面的有符号距离就是 $H(P) = n \cdot P + D$。距离为正表示点在法向量指向的一侧,为负表示在另一侧,为零表示点在平面上。
求交计算: 为了找到光线 $P(t) = R_o + t R_d$ 与平面 $n \cdot P + D = 0$ 的交点,我们将光线方程代入平面方程:
\[n \cdot (R_o + t R_d) + D = 0\]整理得到:
\[n \cdot R_o + t (n \cdot R_d) + D = 0\]解出参数 $t$:
\[t = - \frac{n \cdot R_o + D}{n \cdot R_d}\]注意事项:
- 如果分母 $n \cdot R_d = 0$,表示光线平行于平面。此时,如果分子 $n \cdot R_o + D = 0$,则光线在平面内(无限交点);否则光线与平面不相交。
- 计算出 $t$ 后,必须检查 $t > \epsilon$ ($\epsilon$ 是一个很小的正数,用于避免浮点精度问题),以确保交点在光线的正方向上且不是光线源点自身。
- 交点坐标为 $P_{intersect} = R_o + t R_d$。
光线与三角形 (Triangle) 求交
三角形是计算机图形学中最常用的基本图元,复杂的三维模型通常表示为三角形网格。
- 求交步骤: 光线与三角形的求交通常分两步进行:
- 计算光线与包含该三角形的平面的交点 $P_{intersect}$。如果光线与平面平行或交点在光线反方向,则无交点。
- 判断平面交点 $P_{intersect}$ 是否位于三角形的内部。
重心坐标 (Barycentric Coordinates): 判断点是否在三角形内部的一个常用方法是使用重心坐标。对于三角形 $P_0P_1P_2$,其内部(及边界)的任意一点 $P$ 都可以表示为其顶点的线性组合:
\[P = \alpha P_0 + \beta P_1 + \gamma P_2\]其中,系数 $(\alpha, \beta, \gamma)$ 称为点 $P$ 相对于三角形 $P_0P_1P_2$ 的重心坐标。它们满足以下条件:
\[\alpha \ge 0, \beta \ge 0, \gamma \ge 0\] \[\alpha + \beta + \gamma = 1\]如果一个点 $P$ 的重心坐标 $(\alpha, \beta, \gamma)$ 均在 $[0, 1]$ 区间内,则该点位于三角形内部或边界上。重心坐标还有许多其他应用,如在三角形表面进行纹理坐标、法向量或颜色的平滑插值。
Möller–Trumbore 算法: 这是一种高效的直接计算光线与三角形交点 $t$ 值以及交点重心坐标 $\beta, \gamma$($\alpha = 1 - \beta - \gamma$)的方法。它将光线方程 $R_o + t R_d = (1-\beta-\gamma)P_0 + \beta P_1 + \gamma P_2$ 变形为一个关于 $(t, \beta, \gamma)$ 的线性方程组:
\[R_o - P_0 = \beta (P_1 - P_0) + \gamma (P_2 - P_0) - t (-R_d)\]令 $E_1 = P_1 - P_0$, $E_2 = P_2 - P_0$, $S = R_o - P_0$。则方程组可写为:
\[\begin{pmatrix} -R_d & E_1 & E_2 \end{pmatrix} \begin{pmatrix} t \\ \beta \\ \gamma \end{pmatrix} = S\]可以使用克莱姆法则 (Cramer’s Rule) 或其他方法求解这个 $3 \times 3$ 线性系统。例如,使用克莱姆法则:
\[t = \frac{\det(S, E_1, E_2)}{\det(-R_d, E_1, E_2)}\] \[\beta = \frac{\det(-R_d, S, E_2)}{\det(-R_d, E_1, E_2)}\] \[\gamma = \frac{\det(-R_d, E_1, S)}{\det(-R_d, E_1, E_2)}\]其中 $\det(A, B, C)$ 表示由向量 $A, B, C$ 作为列(或行)构成的矩阵的行列式,也等于混合积 $(A \times B) \cdot C$。 计算出 $(t, \beta, \gamma)$ 后,需要进行有效性检查:
- $t > \epsilon$ (交点在光线正方向)
- $\beta \ge 0$
- $\gamma \ge 0$
- $\beta + \gamma \le 1$ (等价于 $\alpha = 1 - \beta - \gamma \ge 0$) 只有所有条件都满足时,光线才与该三角形相交,交点为 $R_o + t R_d$。
光线与多边形 (Polygon) 求交
尽管三角形最为常用,有时也需要处理一般的(凸或凹)多边形。一个 $n$ 边形可以表示为 $n$ 个顶点的有序列表 ${v_0, v_1, \dots, v_{n-1}}$,这些顶点共面。
- 求交步骤:
- 计算光线与多边形所在平面的交点 $P_{intersect}$。平面方程可以通过前三个不共线的顶点计算得到(例如,法向量 $n = (v_1 - v_0) \times (v_2 - v_0)$)。
- 判断平面交点 $P_{intersect}$ 是否位于多边形的内部。
- 点在多边形内判断 (2D): 为了执行第 2 步,通常将多边形和交点 $P_{intersect}$ 投影到一个二维平面(如 XY, YZ 或 XZ 平面,选择投影面积最大的那个以避免退化)。然后,在二维平面上判断投影点 $P’$ 是否在投影多边形 $V’$ 的内部。常用的方法有:
- 射线投射法 (Crossing Test / Odd-Even Rule): 基于 Jordan 曲线定理。从待测点 $P’$ 发出一条任意方向的射线(通常选择水平正方向),计算该射线与多边形边界的交点个数。如果交点个数为奇数,则点在多边形内部;如果为偶数,则点在外部。需要小心处理射线穿过顶点或与边重合的特殊情况。
- 实现: 将坐标原点移至 $P’$。以 X 轴正半轴为射线。遍历多边形的每条边 $(v'_i, v'_{i+1})$ (注意 $v'_n = v'_0$)。如果边的两个端点的 Y 坐标异号(一个正一个负),则该边可能与 X 轴正半轴相交。计算该边与 X 轴的交点 $x_{intersect}$。如果 $x_{intersect} > 0$,则计数器加 1。最后检查计数器的奇偶性。
- 环绕数法 / 弧长法 (Winding Number / Arc Length Method): 计算多边形相对于待测点 $P’$ 的环绕数。可以想象从 $P’$ 出发观察多边形的顶点,当顶点按顺序绕 $P’$ 移动时,计算总的角度变化。如果总角度变化为 $\pm 2\pi$ 的非零整数倍,则点在内部;如果为 0,则点在外部。
- 基于顶点符号的弧长累加: 这是一种避免直接计算反三角函数的改进方法。将坐标原点移到 $P’$。记录每个顶点 $v'_i = (x_i, y_i)$ 的坐标符号对 $(sx_i, sy_i)$(+ 或 -,0 视为 +)。当从 $v'_i$ 移动到 $v'_{i+1}$ 时,根据符号对的变化(跨越象限),累加相应的角度变化量(通常是 $\pm \pi/2$ 或 $\pm \pi$ 的倍数)。特殊处理跨越对角象限的情况(使用 $f = x_i y_{i+1} - x_{i+1} y_i$ 的符号判断增加或减少 $\pi$)。最终累加的总角度如果是 $\pm 2\pi$,则点在内部。此方法相对鲁棒但实现细节较复杂。
- 射线投射法 (Crossing Test / Odd-Even Rule): 基于 Jordan 曲线定理。从待测点 $P’$ 发出一条任意方向的射线(通常选择水平正方向),计算该射线与多边形边界的交点个数。如果交点个数为奇数,则点在多边形内部;如果为偶数,则点在外部。需要小心处理射线穿过顶点或与边重合的特殊情况。
光线与球面 (Sphere) 求交
球面是另一种常见的几何图元。
球面的表示: 由球心 $P_c = (x_c, y_c, z_c)$ 和半径 $r$ 定义。其隐式方程为:
\[(P - P\_c) \cdot (P - P\_c) = r^2\]或者 $|P - P_c|^2 = r^2$。
代数求解法: 将光线方程 $P(t) = R_o + t R_d$ 代入球面方程:
\[(R\_o + t R\_d - P\_c) \cdot (R\_o + t R\_d - P\_c) = r^2\]令 $L = R_o - P_c$(从球心指向光线起点的向量)。方程变为: \((L + t R\_d) \cdot (L + t R\_d) = r^2\)
展开得到:
\[(R\_d \cdot R\_d) t^2 + 2 (L \cdot R\_d) t + (L \cdot L - r^2) = 0\]这是一个关于 $t$ 的一元二次方程 $at^2 + bt + c = 0$,其中:
- $a = R_d \cdot R_d$ (如果 $R_d$ 是单位向量,则 $a=1$)
- $b = 2 (L \cdot R_d) = 2 (R_o - P_c) \cdot R_d$
- $c = L \cdot L - r^2 = (R_o - P_c) \cdot (R_o - P_c) - r^2$ 通过求解判别式 $\Delta = b^2 - 4ac$ 来判断交点情况:
- $\Delta < 0$: 光线与球面不相交。
- $\Delta = 0$: 光线与球面相切,有一个交点,$t = -b / (2a)$。
- $\Delta > 0$: 光线与球面相交于两点,$t_{1,2} = \frac{-b \pm \sqrt{\Delta}}{2a}$。 在光线跟踪中,我们通常关心的是沿光线方向的第一个交点,即 $t$ 值最小且 $t > \epsilon$ 的那个解。
几何求解法: 这种方法更直观,有时可以更快地排除不相交的情况。
- 计算从球心 $P_c$ 指向光线起点 $R_o$ 的向量 $L = R_o - P_c$。
- 检查起点位置:
- 如果 $L \cdot L < r^2$,则光线起点在球内部。
- 如果 $L \cdot L = r^2$,则光线起点在球面上。
- 如果 $L \cdot L > r^2$,则光线起点在球外部。
- 计算 $L$ 在光线方向 $R_d$ 上的投影长度 $t_p = - (L \cdot R_d) / (R_d \cdot R_d)$(如果 $|R_d|=1$, $t_p = -L \cdot R_d$)。$t_p$ 对应光线上距离球心最近的点的参数。
- 快速排除 (起点在外部): 如果光线起点在球外部 ($L \cdot L > r^2$) 且 $t_p < 0$(最近点在光线反方向),则光线背离球面,不相交。
- 计算球心到光线(直线)的垂直距离的平方 $d^2 = L \cdot L - t_p^2 (R_d \cdot R_d)$ (如果 $|R_d|=1$, $d^2 = L \cdot L - t_p^2$)。
- 检查距离: 如果 $d^2 > r^2$,则光线与球面不相交。
- 计算从最近点到交点的弦长的一半的平方 $t’^2 = r^2 - d^2$。
- 计算交点参数 t:
- 如果起点在球外部 ($L \cdot L > r^2$):第一个交点是 $t = t_p - \sqrt{t'^2 / (R_d \cdot R_d)}$ (如果 $|R_d|=1$, $t = t_p - \sqrt{t'^2}$)。
- 如果起点在球内部 ($L \cdot L < r^2$):只有一个正的交点 $t = t_p + \sqrt{t'^2 / (R_d \cdot R_d)}$ (如果 $|R_d|=1$, $t = t_p + \sqrt{t'^2}$)。
- 如果起点在球面上,需特殊处理。
光线与长方体 (Box) 求交
长方体(尤其是轴对齐长方体 Axis-Aligned Bounding Box, AABB)在图形学中非常重要,常用作复杂物体的包围盒 (Bounding Box),用于加速光线求交。如果光线连包围盒都碰不到,那它肯定碰不到内部的复杂物体。
Slab 方法 (Kay and Kajiya / Haines): 一个长方体可以看作是三对互相平行的平面(称为 Slabs)的交集。例如,一个 AABB 由 $x=x_{min}, x=x_{max}$; $y=y_{min}, y=y_{max}$; $z=z_{min}, z=z_{max}$ 六个平面界定。 该算法分别计算光线与构成每个 Slab 的两个平行平面的交点参数 $t$。对于第 $i$ 个 Slab($i=0, 1, 2$ 对应 x, y, z 轴),设光线进入该 Slab 的参数为 $t_{min}^{(i)}$,离开的参数为 $t_{max}^{(i)}$ (需要考虑光线方向,可能 $t_{min}^{(i)} > t_{max}^{(i)}$,此时需要交换它们)。 然后,计算光线同时位于所有三个 Slab 内部的参数区间 $[t_{min}, t_{max}]$:
\[t_{min} = \max(t_{min}^{(0)}, t_{min}^{(1)}, t_{min}^{(2)})\] \[t_{max} = \min(t_{max}^{(0)}, t_{max}^{(1)}, t_{max}^{(2)})\]光线与长方体相交当且仅当 $t_{min} < t_{max}$ 且 $t_{max} > \epsilon$。如果相交,光线射入长方体的参数是 $t_{min}$(如果 $t_{min} > \epsilon$)或 0(如果光线起点在内部),射出的参数是 $t_{max}$。 这个思想与 Liang-Barsky 线段裁剪算法 类似。
Woo 算法 (针对 AABB): Andrew Woo 提出了一种针对 AABB 的优化算法 [Andrew Woo, “Fast ray–box intersection”, 1990]。它首先根据光线方向 $R_d$ 的符号,确定对于每个轴 (x, y, z),光线将首先遇到哪个平面($min$ 平面还是 $max$ 平面)。这三个首先遇到的平面称为“近平面”。然后,计算光线与这三个近平面的交点参数 $t_x, t_y, t_z$。取其中最大的一个 $t_{candidate} = \max(t_x, t_y, t_z)$ 作为潜在的入口交点参数。最后,计算出潜在交点 $P_{candidate} = R_o + t_{candidate} R_d$,并检查该点是否确实位于长方体的表面上(即,其另外两个坐标是否在长方体对应的区间内)。如果检查通过且 $t_{candidate} > \epsilon$,则 $t_{candidate}$ 就是第一个交点的参数;否则不相交。
掌握了基本的光线求交技术后,我们就可以构建光线跟踪算法了。
经典光线跟踪算法
光线跟踪算法有多种变体,复杂度 和 能够模拟的效果 各不相同。
算法对比
- 光线投射 (Ray Casting): 最简单形式。只计算从视点发出的主光线 (primary ray) 与场景的第一个交点,并根据该点的局部光照模型(考虑光源直接照射)计算颜色。不支持阴影、反射、折射等全局效果。
- Whitted-Style 光线跟踪 (Recursive Ray Tracing): Whitted 提出的经典算法。在光线投射的基础上,当主光线击中物体表面时,递归地跟踪反射光线(如果表面是反射的)和折射光线(如果表面是透明的),并将它们贡献的颜色按相应系数(反射/折射系数)累加到最终颜色上。能够产生清晰的反射和折射效果,以及硬阴影。
- 局限性: 只能处理理想镜面反射和折射,无法模拟模糊(光泽/glossy)反射/折射。对于漫反射 (diffuse) 表面,它只考虑直接光照,不考虑从其他漫反射表面反射过来的间接光照 (indirect lighting)。
- 蒙特卡洛光线跟踪 / 路径追踪 (Monte Carlo Ray Tracing / Path Tracing): 更高级、更物理真实的方法。它将渲染视为求解渲染方程 (Rendering Equation) 这个积分方程。路径追踪使用蒙特卡洛方法来估计这个积分:在每次光线与表面交互时,根据表面的材质属性(BRDF)随机地采样一个新的方向继续追踪光线。通过平均大量从像素出发的随机光线路径的贡献,可以得到物理上更准确的结果。
- 优势: 天然支持各种复杂材质(漫反射、光泽反射/折射、混合材质)、间接光照、软阴影、景深、运动模糊等效果。
- 劣势: 收敛速度慢,需要大量采样才能减少噪点 (noise)。难以高效处理某些特定的光路,特别是焦散 (Caustics) 效果(光线通过聚焦或反射汇聚在漫反射表面上形成亮斑)。
光线投射 (Ray Casting)
这是光线跟踪算法的最基本形式。
算法流程:
- 对于屏幕(视窗)上的每一个像素: a. 构造一条从视点 (eye/camera position) 出发,穿过该像素中心的光线 $P(t) = R_o + t R_d$。 b. 遍历场景中的所有物体,计算该光线与每个物体的交点。 c. 找到所有交点中 $t$ 值最小且 $t > \epsilon$ 的那个交点,即距离视点最近的可见交点 $P_{intersect}$。 d. IF 找到了交点: i. 获取交点处的表面法向量 $N$ 和材质属性。 ii. 使用局部光照模型(例如 Phong 或 Blinn-Phong 模型)计算颜色。这通常包括环境光 (ambient) 项,以及对每个光源计算漫反射 (diffuse) 和高光 (specular) 项。 iii. 将计算得到的颜色赋给该像素。 e. ELSE (没有找到交点): i. 将背景颜色赋给该像素。
伪代码
FOR each pixel (x, y) in image:
ray = constructRayThroughPixel(eye, x, y)
nearest_t = infinity
nearest_object = null
FOR each object in scene:
t = intersect(ray, object)
IF t > epsilon AND t < nearest_t:
nearest_t = t
nearest_object = object
IF nearest_object is not null:
intersection_point = ray.origin + nearest_t * ray.direction
normal = nearest_object.getNormal(intersection_point)
material = nearest_object.getMaterial(intersection_point)
pixel_color = material.ambient_color * global_ambient_light
FOR each light_source in scene:
// Calculate diffuse and specular contribution from this light
// (Assuming Phong model for simplicity)
light_direction = normalize(light_source.position - intersection_point)
view_direction = normalize(eye - intersection_point)
// Diffuse term
diffuse_intensity = max(0, dot(normal, light_direction))
pixel_color += material.diffuse_color * light_source.color * diffuse_intensity
// Specular term
reflection_direction = reflect(-light_direction, normal)
specular_intensity = pow(max(0, dot(view_direction, reflection_direction)), material.shininess)
pixel_color += material.specular_color * light_source.color * specular_intensity
setPixelColor(x, y, pixel_color)
ELSE:
setPixelColor(x, y, background_color)
局限性: 光线投射只考虑了光线从光源直接到物体表面再到眼睛的路径(或反向路径),没有考虑光线在场景中的进一步弹射。因此,它无法生成阴影、镜面反射和透明折射效果。
添加阴影 (Shadows)
阴影是判断一个点是否能被特定光源照亮。可以在光线投射的基础上通过引入阴影光线 (Shadow Rays) 来实现:
- 在计算某个光源对交点 $P_{intersect}$ 的贡献之前: a. 构造一条从 $P_{intersect}$ 出发,指向该光源位置的阴影光线。设其方向为 $L$。 b. 对场景中的所有物体(除了光源自身和当前物体有时可以排除外)进行求交测试,看阴影光线在到达光源之前是否与任何物体相交。 c. IF 阴影光线在到达光源的距离内 ($0 < t_{shadow} < distance_to_light$) 与任何物体相交: i. 则该点 $P_{intersect}$ 对于此光源处于阴影中,该光源对此点的直接光照贡献(漫反射和高光)为 0。 d. ELSE (阴影光线未被遮挡): i. 该点被此光源照亮,正常计算其漫反射和高光贡献。
注意: 对于阴影光线求交,我们只需要知道是否存在任何遮挡物,而不需要找到最近的交点,因此可以在找到第一个遮挡物后立即停止该光源的阴影测试(优化)。
伪代码 (带阴影):
// ... (inside the IF nearest_object is not null block) ...
pixel_color = material.ambient_color * global_ambient_light
FOR each light_source in scene:
light_direction = normalize(light_source.position - intersection_point)
distance_to_light = length(light_source.position - intersection_point)
// Cast shadow ray
shadow_ray_origin = intersection_point + epsilon * normal // Offset origin slightly
shadow_ray = Ray(shadow_ray_origin, light_direction)
is_in_shadow = false
FOR each object_k in scene: // Check for occlusion
t_shadow = intersect(shadow_ray, object_k)
IF t_shadow > epsilon AND t_shadow < distance_to_light:
is_in_shadow = true
BREAK // Found an occluder, no need to check further for this light
IF not is_in_shadow:
// Calculate and add diffuse and specular contribution from this light
view_direction = normalize(eye - intersection_point)
// ... (Phong calculation as before) ...
pixel_color += /* diffuse term */ + /* specular term */
setPixelColor(x, y, pixel_color)
// ... (rest of the algorithm) ...
Whitted-Style 光线跟踪 (Recursive Ray Tracing)
Whitted 的方法将光线投射提升到了一个新的层次,通过递归地跟踪反射和折射光线来模拟镜面效果。
核心思想:
当一条光线 $I$ 击中一个表面点 $P$ 时,除了计算该点的局部光照颜色外,还需要考虑:
- 反射: 如果表面具有反射属性(由材质的反射系数 $k_r$ 决定),则根据反射定律计算出反射光线的方向 $R$,并递归地调用光线跟踪函数来计算该反射光线 $Ray(P, R)$ 所带来的颜色 $Color_R$。最终颜色会加上 $k_r \times Color_R$。
- 折射: 如果表面具有透明/折射属性(由材质的折射系数 $k_t$ 和相对折射率 $\eta$ 决定),则根据斯涅尔定律 (Snell’s Law) 计算出折射光线的方向 $T$,并递归地调用光线跟踪函数来计算该折射光线 $Ray(P, T)$ 所带来的颜色 $Color_T$。最终颜色会加上 $k_t \times Color_T$。
反射定律 (Law of Reflection):
- 入射角等于反射角 ($\theta_i = \theta_r$)。
- 入射光线 $I$、表面法向量 $N$ 和反射光线 $R$ 位于同一个平面内。 反射光线方向向量 $R$ 可以由入射光线方向向量 $I$(指向表面)和单位法向量 $N$ 计算得出:
这里假设 $I$ 是指向交点的方向。如果 $I$ 是从交点出发的方向(通常在光线跟踪中是这样定义的),则公式变为:
\[R = I - 2 (N \cdot I) N \quad \text{(if } I \text{ points away from surface)}\]或者更常用的,如果 $I$ 是入射方向(指向表面),$V = -I$ 是从表面出发的入射向量,则反射方向 $R$ (从表面出发) 是:
\[R = -V + 2 (N \cdot V) N\]或者使用指向表面的 $I$:
\[R_{out} = R_{in} - 2 \text{dot}(N, R_{in}) N\]其中 $R_{in}$ 是指向表面的入射光线方向,$N$ 是表面法线,$R_{out}$ 是反射光线的方向。
折射定律 (Snell’s Law): 当光线从折射率为 $\eta_i$ 的介质进入折射率为 $\eta_t$ 的介质时:
- $\eta_i \sin \theta_i = \eta_t \sin \theta_t$,其中 $\theta_i$ 是入射角,$\theta_t$ 是折射角(均相对于法线)。
- 入射光线 $I$、表面法向量 $N$ 和折射光线 $T$ 位于同一个平面内。 折射光线方向向量 $T$ 可以根据入射向量 $I$ (指向表面)、单位法向量 $N$ 以及相对折射率 $\eta = \eta_i / \eta_t$ 计算。设 $c_1 = -N \cdot I$ (即 $\cos \theta_i$)。根据斯涅尔定律 $\sin^2 \theta_t = (\eta_i / \eta_t)^2 \sin^2 \theta_i = \eta^2 (1 - \cos^2 \theta_i) = \eta^2 (1 - c_1^2)$。令 $c_2 = \sqrt{1 - \eta^2 (1 - c_1^2)}$ (即 $\cos \theta_t$)。折射向量 $T$ (从表面出发) 为:
全内反射 (Total Internal Reflection): 如果 $1 - \eta^2 (1 - c_1^2) < 0$,即 $\eta \sin \theta_i > 1$(只在 $\eta_i > \eta_t$ 时可能发生),则光线无法折射,会发生全内反射,此时只计算反射光线。
递归框架:
Whitted-Style 光线跟踪通常以递归函数的形式实现。
伪代码 (Recursive IntersectColor):
function IntersectColor(ray, depth):
IF depth > MAX_DEPTH:
return BLACK // Stop recursion
find nearest intersection (t, object) for ray
IF no intersection:
return BACKGROUND_COLOR
intersection_point = ray.origin + t * ray.direction
normal = object.getNormal(intersection_point)
material = object.getMaterial(intersection_point)
view_direction = -ray.direction
// Calculate Local Illumination (Ambient + Diffuse + Specular)
local_color = CalculateLocalIllumination(intersection_point, normal, view_direction, material)
reflected_color = BLACK
refracted_color = BLACK
// Calculate Reflection
IF material.reflectivity > 0:
reflection_direction = reflect(-view_direction, normal)
reflection_ray_origin = intersection_point + epsilon * normal // Offset
reflection_ray = Ray(reflection_ray_origin, reflection_direction)
reflected_color = IntersectColor(reflection_ray, depth + 1)
// Calculate Refraction
IF material.transparency > 0:
refraction_direction = refract(-view_direction, normal, material.refractive_index)
IF refraction_direction is valid: // Check for total internal reflection
// Determine origin offset direction (entering or exiting?)
IF dot(normal, view_direction) > 0: // Ray hits from outside
refraction_ray_origin = intersection_point - epsilon * normal
ELSE: // Ray hits from inside
refraction_ray_origin = intersection_point + epsilon * normal
refraction_ray = Ray(refraction_ray_origin, refraction_direction)
refracted_color = IntersectColor(refraction_ray, depth + 1)
ELSE: // Total internal reflection occurs, treat as reflection
// (Optionally, add this reflection to the reflected_color computed above,
// or handle it exclusively if transparency was intended but failed)
// For simplicity here, we might just rely on the main reflection calculation
pass // Or compute TIR reflection and add/replace
// Combine colors
final_color = local_color + material.reflectivity * reflected_color + material.transparency * refracted_color
return final_color
// Main loop calls IntersectColor(primary_ray, 0) for each pixel
递归终止条件: 为了防止无限递归(例如光线在两个镜子之间来回反射),必须设定终止条件:
- 最大递归深度 (Max Depth): 限制光线弹射的最大次数。当递归层数达到预设阈值时停止。
- 贡献阈值 (Contribution Threshold): 当光线的贡献(由于每次反射/折射的能量损失,即系数 $k_r, k_t < 1$)衰减到低于某个很小的值时停止。
下图展示了不同递归深度下的渲染效果:
添加纹理 (Texture Mapping): 为了增加场景的真实感和细节,可以在物体表面应用纹理。在光线与物体表面相交时,需要计算交点 $P_{intersect}$ 对应的纹理坐标 (UV coordinates)。这通常通过插值得到(例如,对于三角形,使用交点的重心坐标插值顶点纹理坐标)。然后,使用这个纹理坐标到纹理图像(二维纹理)或程序化函数(三维纹理)中查找颜色、法线扰动(凹凸贴图/法线贴图)或其他材质属性,并在计算局部光照或决定反射/折射行为时使用这些从纹理中获取的值。
蒙特卡洛光线跟踪 / 路径追踪 (Monte Carlo Ray Tracing / Path Tracing)
Whitted-Style 光线跟踪虽然能产生清晰的反射和折射,但其模型过于简化,无法处理更普遍的现象,如:
- 模糊反射/折射 (Glossy surfaces)。
- 漫反射表面之间的相互反射(间接光照,Color Bleeding)。
蒙特卡洛光线跟踪(通常实现为路径追踪)通过一种更基于物理、概率驱动的方式来解决这些问题。
核心思想:
渲染方程 (Rendering Equation) 描述了场景中某点 $x$ 沿某一方向 $\omega_o$ 的出射光亮度 $L_o(x, \omega_o)$:
\[L_o(x, \omega_o) = L_e(x, \omega_o) + \int_{\Omega} f_r(x, \omega_i, \omega_o) L_i(x, \omega_i) (\omega_i \cdot n) d\omega_i\]其中:
- $L_e$ 是点 $x$ 自身发出的光(光源)。
- $f_r$ 是表面的 双向反射分布函数 (BRDF),描述了光线从 $\omega_i$ 方向入射后,有多少能量被反射到 $\omega_o$ 方向。
- $L_i(x, \omega_i)$ 是从 $\omega_i$ 方向入射到点 $x$ 的光亮度。
- $\Omega$ 是覆盖点 $x$ 表面法线 $n$ 的整个半球。
- $(\omega_i \cdot n)$ 是考虑入射角余弦的投影因子。
这个方程是递归的:入射光 $L_i(x, \omega_i)$ 来自于场景中其他点 $x’$ 的出射光 $L_o(x’, -\omega_i)$。直接求解这个积分方程通常非常困难。
蒙特卡洛方法: 路径追踪使用蒙特卡洛积分来近似求解渲染方程中的积分项。其基本思路是:
- 从视点通过像素发射一条光线。
- 当光线击中表面 $x$ 时,不再像 Whitted 那样确定性地分裂成反射和折射光线,而是根据表面的 BRDF $f_r$ 随机地采样一个入射方向 $\omega_i$(或者说,采样一个新的出射方向 $\omega_o’$)。
- 向采样到的新方向 $\omega_o’$ 发射下一条光线,递归地追踪这条光线,得到其贡献的亮度 $L_{recursive}$。
- 当前点的亮度贡献近似为 $\frac{f_r(x, \omega_i, \omega_o) L_{recursive} (\omega_i \cdot n)}{p(\omega_i)}$,其中 $p(\omega_i)$ 是采样方向 $\omega_i$ 的概率密度函数 (PDF)。为了提高效率,通常采用重要性采样 (Importance Sampling),即优先采样 BRDF 值较大或入射光较强的方向。
- 俄罗斯轮盘赌 (Russian Roulette): 为了在有限步数内终止路径追踪,当光线能量衰减到一定程度时,以一定概率 $p$ 继续追踪,并将贡献乘以 $1/p$;以 $1-p$ 的概率终止追踪。
路径追踪流程:
- 对于每个像素,重复 $N$ 次($N$ 是每个像素的样本数): a. 从视点发射一条穿过该像素(可能带有随机抖动以抗锯齿)的光线。 b. 初始化路径贡献 $C = (1, 1, 1)$ 和路径亮度 $L = (0, 0, 0)$。 c. 循环 (追踪路径): i. 找到光线与场景的最近交点 $x$。 ii. 如果没有交点或达到最大深度,跳出循环。 iii. 如果交点是光源,累加光源亮度 $L += C \times L_e(x, -\omega)$。 iv. 根据交点 $x$ 的材质 BRDF $f_r$ 和入射方向 $-\omega$,随机采样一个新的方向 $\omega’$。 v. 计算采样方向的 PDF $p(\omega’)$。 vi. 更新路径贡献 $C *= \frac{f_r(x, -\omega, \omega’) (\omega’ \cdot n)}{p(\omega’)}$。 vii. 使用俄罗斯轮盘赌决定是否继续追踪。如果终止,跳出循环。如果继续,更新 $C$ 并构造新的光线 $Ray(x + \epsilon n, \omega’)$。 d. 将本次路径得到的总亮度 $L$ 累加到像素的总亮度上。
- 将每个像素的总亮度除以样本数 $N$,得到最终像素颜色。
优势与效果:
路径追踪能够自然地模拟广泛的全局光照效果,因为它直接尝试模拟光在场景中的随机游走:
- 间接漫反射 (Indirect Diffuse Illumination): 光线在漫反射表面之间的多次反弹,如著名的 Color Bleeding 效果(一个有色物体会将其颜色“染”到附近的白色表面上)。
- 软阴影 (Soft Shadows): 由面光源或区域光源产生的阴影,边缘有自然的半影区。
- 光泽反射/折射 (Glossy Reflection/Refraction): 模糊的反射和折射,由非理想镜面或磨砂玻璃产生。
- 景深 (Depth of Field): 模拟相机镜头聚焦效果。
- 运动模糊 (Motion Blur): 模拟快速移动物体的模糊轨迹。
缺点:
- 噪点 (Noise): 由于蒙特卡洛采样的随机性,需要大量的样本 ($N$ 很大) 才能使结果收敛,减少可见的噪点。收敛速度慢是其主要缺点。
- 性能: 计算量非常大,实时应用需要强大的硬件和/或先进的降噪技术。
- 难以处理焦散 (Caustics): 焦散是由光线通过镜面反射或折射后汇聚到漫反射表面上形成的亮斑(例如,光透过玻璃杯在桌面上形成的光斑)。标准的路径追踪很难采样到这些特定的、间接的 specular-diffuse 光路,导致焦散效果渲染效率低下或缺失。
处理焦散的进阶技术:
为了更好地渲染焦散等困难光路,发展了一些更复杂的算法,如:
- 双向路径追踪 (Bidirectional Path Tracing, BDPT): 同时从相机和光源发出路径,并在中间连接它们,提高了采样困难光路的概率。
- 光子映射 (Photon Mapping): 一个两阶段方法。第一阶段 (Photon Tracing) 从光源发射大量“光子”,记录它们在场景中撞击表面的位置和能量(构建光子图)。第二阶段 (Rendering) 从相机发射光线,在交点处利用附近的光子信息来估计间接光照和焦散。
- 顶点连接与合并 (Vertex Connection and Merging, VCM) / 统一路径采样 (Unified Path Sampling, UPS): 结合了 BDPT 和 Photon Mapping 的优点。
感兴趣的读者可以参考 2003 年 SIGGRAPH 的课程笔记 “Monte Carlo Ray Tracing”。
光线跟踪的一些思考与挑战
在实现和应用光线跟踪时,会遇到一些实际问题和挑战。
自遮挡 / 表面痤疮 (Self-Occlusion / Surface Acne)
由于浮点数计算的精度限制,光线与表面计算出的交点 $P_{intersect}$ 可能并不精确地位于表面上,而是稍微陷入表面内部或浮于表面之上。当从这个不精确的 $P_{intersect}$ 发射次级光线(反射、折射或阴影光线)时:
- 如果 $P_{intersect}$ 在表面内部,次级光线可能立即再次与同一表面相交,导致错误的自遮挡(例如,阴影光线认为自己被挡住了,产生黑色斑点)。
- 如果 $P_{intersect}$ 在表面外部,次级光线可能与本应离开的表面产生错误的“间隙”。
解决方案: 在发射次级光线时,将光线的源点沿表面法线方向(或光线方向)微移一个很小的距离 $\epsilon$ (epsilon offset):
- 对于反射光线和离开表面的折射光线,沿法线 $N$ 方向移动:$Origin_{new} = P_{intersect} + \epsilon N$。
- 对于进入表面的折射光线,沿法线反方向移动:$Origin_{new} = P_{intersect} - \epsilon N$。
- 对于阴影光线,通常沿法线 $N$ 方向移动。
选择合适的 $\epsilon$ 值很重要,太小可能无法解决问题,太大可能导致光线“跳过”场景中薄的物体。
退化情况 / 特殊情况 (Degenerate Cases)
光线求交计算需要小心处理各种特殊或退化情况,例如:
- 光线与平面或球面相切。
- 光线穿过三角形的顶点或边。
- 光线与 AABB 的边或顶点相交。
- 除数为零的情况(如光线平行于平面)。 健壮的实现需要识别并正确处理这些情况,以避免 NaN (Not a Number) 或错误的计算结果。
加速结构 (Acceleration Structures)
对场景中的每个物体都进行光线求交测试是非常低效的,尤其是当场景包含数百万个三角形时。为了加速求交过程,需要使用空间数据结构来快速剔除与光线路径无关的大部分物体。常见的加速结构包括:
- 包围盒层次结构 (Bounding Volume Hierarchy, BVH): 将物体组织在一个树状结构中,每个节点包含一个简单的包围体(如 AABB 或球体),包围其所有子节点的物体或包围体。光线遍历 BVH 时,如果它不与节点的包围体相交,则可以跳过该节点下的整个子树。
- k-d 树 (k-dimensional tree): 递归地用轴对齐的平面将空间划分为子空间,并将物体分配给它们所在的子空间。
- 均匀网格 (Uniform Grid) / 空分八叉树 (Spatial Octree): 将空间划分为规则的单元格,每个单元格存储与之重叠的物体列表。光线可以“行走”于这些单元格之间,只对当前单元格内的物体进行测试。
使用加速结构可以将光线求交的复杂度从与物体数量成线性关系 $O(N)$ 降低到对数关系 $O(\log N)$ 或更好,这对于处理复杂场景至关重要。
物理准确性 vs. 视觉效果
虽然光线跟踪常被认为更“物理准确”,但需要注意:
- 反向追踪: 大多数光线跟踪算法是从视点向场景反向追踪光线,这与真实光子从光源出发的物理过程相反。这样做效率更高,因为绝大多数从光源出发的光子永远不会到达视点。双向路径追踪等方法试图结合正向和反向追踪。
- 简化与技巧 (Tricks): 有时为了效率或特定的视觉效果,光线跟踪实现可能会采用一些并非严格物理的简化。例如,在计算半透明物体的阴影时,可能只是简单地将穿过物体的光线颜色乘以一个透明度因子,而忽略了光线在物体内部发生的复杂散射和折射路径对阴影形状和颜色的影响。
重要的是理解算法的假设和局限性,并根据应用需求(追求物理精度还是视觉效果和性能)做出选择。
结语
光线跟踪作为一种强大的真实感渲染技术,通过模拟光线的物理传播路径,能够生成极为逼真的图像效果,涵盖精确阴影、反射、折射以及复杂的全局光照现象。从基础的光线投射,到经典的 Whitted-Style 递归光线跟踪,再到基于蒙特卡洛方法的路径追踪,光线跟踪算法不断发展,其能力和应用范围也在持续扩展。尽管面临计算量大、收敛慢、需要处理精度问题和加速等挑战,但随着硬件性能的提升和算法的不断创新,光线跟踪正越来越多地应用于电影、动画、建筑可视化乃至实时游戏等领域,持续推动着计算机图形学的边界。