人工智能中的搜索算法

在计算机科学和人工智能领域，”搜索”是一个基础且核心的概念。许多看似复杂的问题，从自动驾驶汽车规划路径，到解决逻辑谜题，再到优化资源分配，其本质都可以抽象为一个搜索问题。本文将深入探讨什么是搜索问题，介绍几种核心的搜索策略，并讨论它们的性质和应用。

什么是搜索问题？

想象一下，你想从城市的A点开车到B点。你拥有一张地图（或者使用导航应用），知道当前的起点 S 和期望的终点 T。在这两者之间，存在着一个由道路、交叉口和可能的路线组成的网络。你需要在这个网络中找到一条从 S 到 T 的有效路径，甚至可能是最短或最快的那条。

这就是一个典型的搜索问题。我们可以将其更形式化地定义为：

在一个状态空间 (State Space) 中，寻找一条从初始状态 (Initial State) 到一个或多个目标状态 (Goal State) 的路径 (Path)。

• 状态 (State)：问题在某个时刻的描述。例如，在导航问题中，一个状态就是你当前所在的交叉口或位置。
• 状态空间：问题所有可能状态的集合。地图上所有的交叉口和路段共同构成了状态空间。
• 初始状态 (S₀)：问题的起点。例如，导航开始时的位置 A。
• 目标状态 (Sg)：问题希望达到的状态。例如，导航的目的地 B。
• 动作 (Action) / 操作符 (Operator)：从一个状态转移到另一个状态的方式。例如，在路口选择一条特定的道路行驶。
• 路径 (Path)：从初始状态开始，通过一系列动作到达某个状态的状态序列。
• 解路径 (Solution Path)：从初始状态到达目标状态的路径。
• 耗散值 (Cost)：执行一个动作或走过一段路径所付出的代价。例如，导航中的行驶距离、时间或油耗。

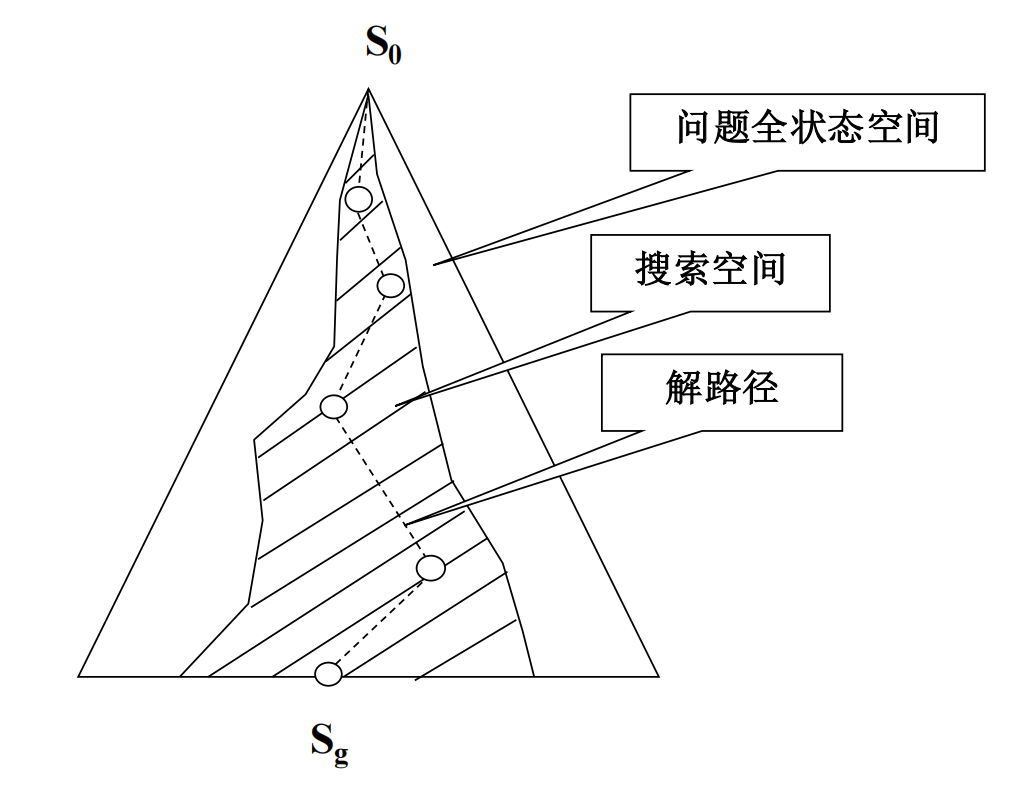
搜索空间 (Search Space) 通常指在求解过程中实际探索过的状态空间部分。理想情况下，我们希望搜索空间远小于整个问题全状态空间，以提高效率。

图中 S0 代表初始状态，Sg 代表目标状态。整个椭圆代表问题的所有可能状态（全状态空间），阴影部分代表搜索过程中实际探索的状态（搜索空间），而连接 S0 和 Sg 的虚线则表示找到的一条解路径。

核心挑战：搜索问题的关键在于如何设计一个高效的搜索策略 (Search Strategy)，即如何选择下一个要探索的状态（或称为“扩展”哪个节点），以便能够利用已有的知识（如果可用），尽可能有效地找到问题的解，尤其是最佳解 (Optimal Solution)（例如，成本最低的路径）。

搜索问题的常见例子

搜索问题无处不在，以下是一些经典的例子：

• 地图路径规划：如前所述，在地图上寻找两个地点之间的最佳路线。
• 传教士和野人问题 (Missionaries and Cannibals Problem)：一个经典的逻辑谜题，涉及将若干传教士和野人安全渡河，需要满足特定约束条件（任何时候，任何一岸的野人数不能超过传教士数，除非该岸没有传教士）。状态是两岸的人员分布和船的位置。
• 华容道 (Klotski Puzzle)：一种滑块类益智游戏，目标是通过移动不同形状的滑块，将特定的滑块（通常是最大的“曹操”）移动到指定出口位置。状态是所有滑块的位置布局。
• 八皇后问题 (Eight Queens Puzzle)：在 8x8 的棋盘上放置八个皇后，使得任意两个皇后都不能互相攻击（即不在同一行、同一列或同一对角线上）。状态可以是部分或完整的皇后布局。

我们关心的问题

在研究和评估不同的搜索算法时，我们通常关注以下几个关键问题：

• 有哪些常用的搜索算法？ (What are the common search algorithms?)
• 完备性 (Completeness)：如果问题存在解，该算法保证能找到解吗？ (Can it find a solution if one exists?)
• 最优性 (Optimality)：该算法找到的解一定是最佳解（例如，成本最低）吗？ (Is the found solution optimal?)
• 最优性条件：在什么情况下，该算法可以保证找到最佳解？ (Under what conditions can optimality be guaranteed?)
• 效率 (Efficiency)：算法求解问题需要多少时间和空间资源？通常用时间复杂度和空间复杂度来衡量。 (How efficient is the algorithm in terms of time and space?)

搜索策略分类：盲目搜索 vs. 启发式搜索

根据搜索过程中是否利用与问题相关的特定知识（启发信息）来指导搜索方向，可以将搜索算法大致分为两类：

1. 盲目搜索 (Blind Search / Uninformed Search)：这类算法仅基于问题的定义（状态、动作、初始状态、目标测试），不使用任何关于目标状态位置或路径成本的额外信息来选择下一个要扩展的节点。它们按照预定的策略系统地探索状态空间。
   • 深度优先搜索 (Depth-First Search, DFS)
   • 宽度优先搜索 (Breadth-First Search, BFS)
2. 启发式搜索 (Heuristic Search / Informed Search)：这类算法利用启发函数 (Heuristic Function) 提供的与问题相关的特定知识（例如，估计当前状态到目标的距离或成本），来评估待扩展节点的“前景”，优先选择那些看起来更有希望接近目标的节点。
   • A 算法 (A Algorithm)
   • A* 算法 (A* Algorithm)

核心问题再次出现：如何选择一个节点进行扩展？ 不同的选择策略导致了不同的搜索算法及其特性。

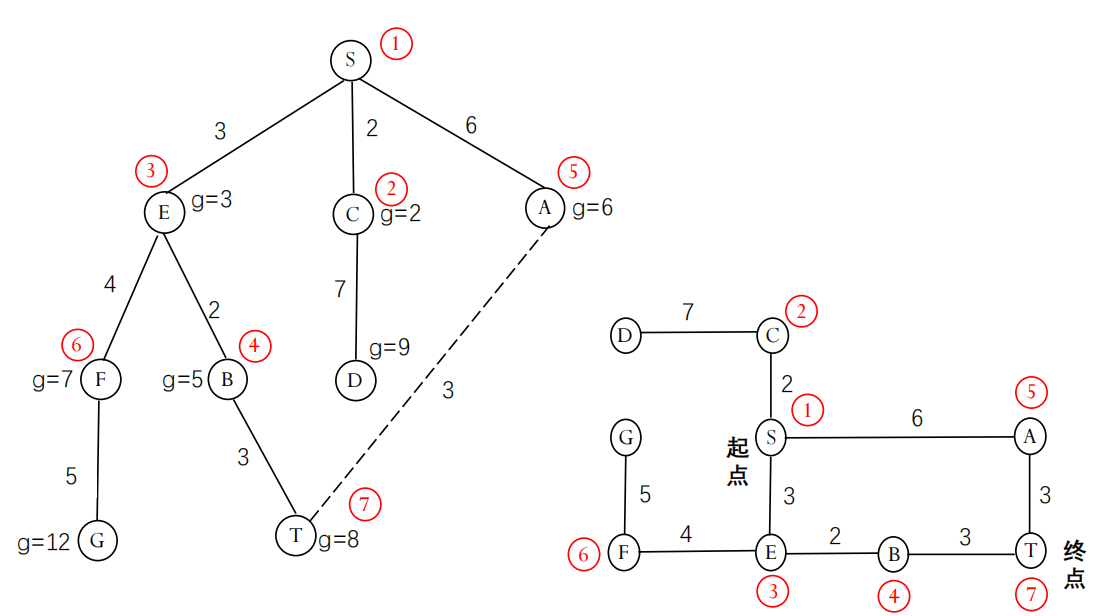
1.1 深度优先搜索 (DFS)

深度优先搜索 (DFS) 的策略是优先扩展搜索树中深度最深的节点。可以想象成尽可能地沿着一条路径往下走，直到遇到死胡同（无法再扩展）或者找到目标，然后才回溯 (Backtrack) 到上一个还有未探索分支的节点，继续深入探索。DFS 通常使用栈 (Stack) 数据结构（显式或隐式地通过递归调用栈）来实现。

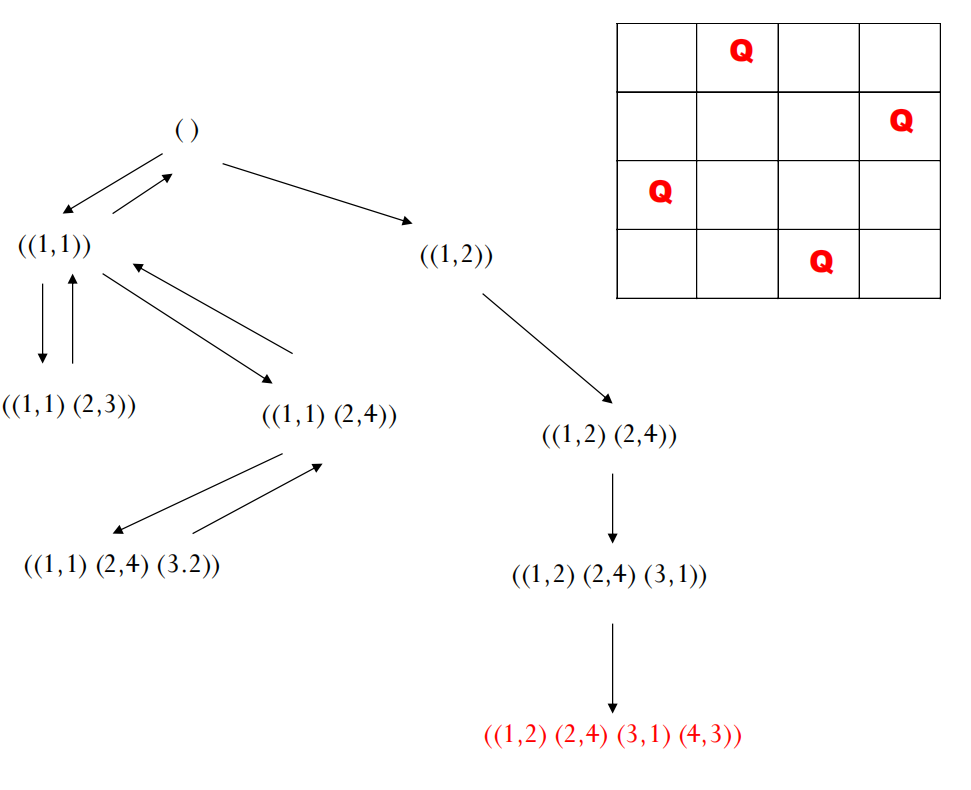
示例：皇后问题

让我们通过四皇后问题来理解 DFS 的过程。状态可以表示为一个元组 ((r1, c1), (r2, c2), ..., (rk, ck))，表示前 k 行皇后的位置。初始状态是 ()。动作是在下一行放置一个不与前面皇后冲突的皇后。

1. 初始状态: () (空棋盘)
2. 扩展: 尝试在第1行放皇后。选择 (1,1)。当前路径/状态: ((1,1))。
3. 继续扩展: 尝试在第2行放皇后。不能放 (2,1), (2,2)。选择 (2,3)。当前路径: ((1,1), (2,3))。
4. 遇到死胡同: 在尝试 ((1,1), (2,3)) 后，发现第3行无处可放。
5. 回溯: 回到上一步 ((1,1))，尝试第2行的下一个可能位置，也就是 (2,4)。当前路径: ((1,1), (2,4))。
6. 继续扩展: 尝试在第3行放皇后。只能放 (3,2)。当前路径: ((1,1), (2,4), (3,2))。
7. 遇到死胡同: 在尝试 ((1,1), (2,4), (3,2)) 后，发现第4行无处可放。
8. 回溯: 没有其他摆放方式，回退直到 ()。
9. 尝试新分支: 回到 () 后，尝试第1行的下一个可能位置，比如 (1,2)。当前路径: ((1,2))。
10. 再次深入: 从 ((1,2)) 出发，再次尝试第2行，如 (2,4)。当前路径: ((1,2), (2,4))…
11. 继续扩展: 此时能够找到解 ((1,2), (2,4), (3,1), (4,3))。

深度优先搜索的性质

• 最优性：一般不能保证找到最优解。DFS找到的第一个解可能路径很长或成本很高，因为它倾向于深入探索，可能错过浅层更优的解。
• 完备性：在有限状态空间中，DFS是完备的（如果解存在，总能找到）。但在无限状态空间或有环路的状态空间中，如果不加控制（如深度限制或记录已访问状态），DFS 可能会陷入无限循环，从而不完备。当使用深度限制 (Depth Limit) 时，如果限制不合理（小于实际最短解的深度），可能找不到解。可以采用迭代加深深度优先搜索 (Iterative Deepening DFS, IDDFS) 来解决深度限制问题，它反复进行深度受限的DFS，每次增加深度限制。
• 效率：
  • 时间复杂度：最坏情况下，DFS需要探索整个状态空间（或达到深度限制内的所有节点）。如果状态空间的分支因子（每个节点平均有多少子节点）为 b，最大深度为 m，则时间复杂度可能是 $O(b^m)$。
  • 空间复杂度：DFS 的一个显著优点是内存效率高。它只需要存储从初始节点到当前节点的路径上的节点，以及当前路径节点未扩展的兄弟节点。空间复杂度为 $O(bm)$（存储路径）或在只存储路径时为 $O(m)$。
• 通用性：DFS 是一种通用的、与问题细节无关的搜索方法。

练习题

设有三个没有刻度的杯子，分别可以装8升、8升和3升水。初始时，两个8升的杯子装满了水。请问如何在不借助于其他器具的情况下，得到恰好4份4升水？请思考如何用程序实现这个问题（提示：状态可以用三个杯子中的水量 (x, y, z) 表示）。

1.2 宽度优先搜索 (BFS)

宽度优先搜索 (BFS) 的策略是优先扩展搜索树中深度最浅的节点。它首先访问初始节点，然后访问所有离初始节点距离为1的节点，接着是距离为2的节点，以此类推，逐层进行搜索。BFS 通常使用队列 (Queue) 数据结构来实现。

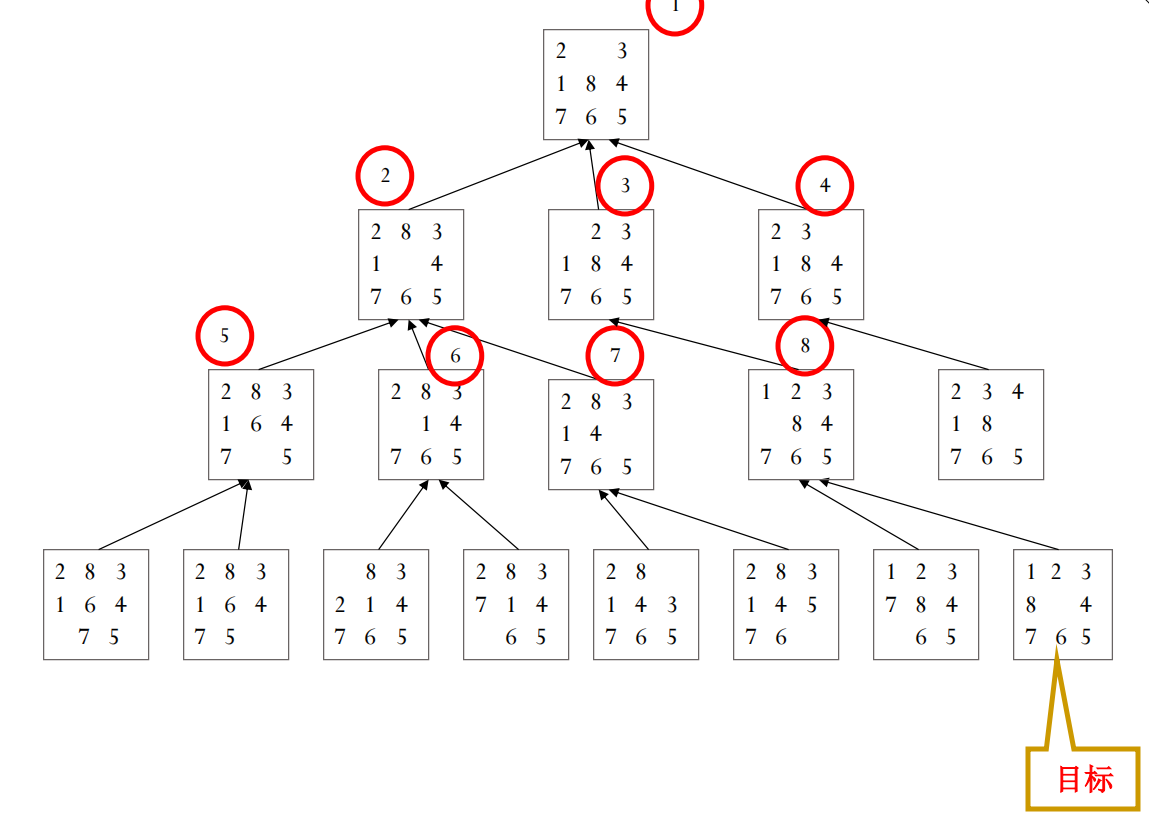
示例：八数码问题 (8-Puzzle)

八数码问题是在 3x3 的棋盘上移动滑块（数字1-8，一个空格），目标是从给定的初始状态达到某个目标状态。BFS 会按层级探索：

1. Level 0: 初始状态 s。
2. Level 1: 所有可以通过一次移动从 s 到达的状态。
3. Level 2: 所有可以通过一次移动从 Level 1 的状态到达，且未在 Level 0 或 Level 1 出现过的状态。
4. …以此类推，直到找到目标状态。

宽度优先搜索的性质

• 最优性：当每一步的耗散值都相等（例如，单位成本，unit cost）时，BFS 保证能找到最优解（即路径最短的解）。因为它按层级扩展，找到的第一个目标节点必然位于最浅的层级，也就是距离初始节点步数最少的路径上。如果成本不一致，BFS找到的不一定是成本最低的解。
• 完备性：只要解存在，BFS 一定能找到解。因为它会系统地探索所有可达节点，不会像DFS那样可能陷入无限深的分支（除非状态空间无限且无解）。
• 效率：
  • 时间复杂度：BFS需要访问所有深度小于等于 d 的节点，其中 d 是最短解的深度。如果分支因子是 b，时间复杂度为 $O(1 + b + b^2 + … + b^d) = O(b^d)$。
  • 空间复杂度：BFS 的主要缺点是空间需求大。它需要存储所有已生成但尚未扩展的节点（队列中的节点）。在最坏情况下，队列可能需要存储第 d 层的所有节点，数量级为 $O(b^d)$。这使得BFS在状态空间非常大时可能因内存耗尽而不可行。
• 通用性：BFS 也是一种通用的、与问题无关的方法。

1.3 迪杰斯特拉算法 (Dijkstra’s Algorithm)

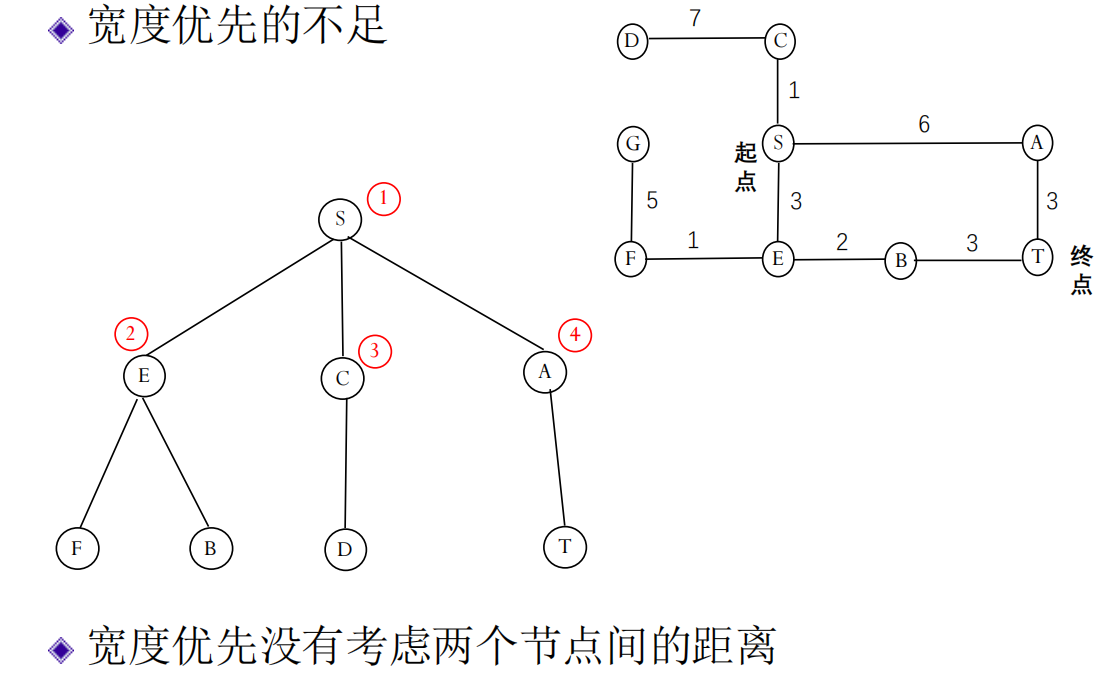
我们看到，当路径成本不一致时，BFS无法保证找到最优解。例如，在地图导航中，不同路段的距离或时间是不同的。BFS只关心经过的节点数（层数），而不关心累积的成本。

为了解决这个问题，迪杰斯特拉算法被提了出来。它是一种用于查找图中单个源点到所有其他顶点的最短路径的算法（适用于非负权边）。在搜索问题的语境下，我们可以用它来找到从初始状态到目标状态的成本最低的路径。

Dijkstra 算法可以看作是 BFS 的一种推广。它也使用一个优先队列 (Priority Queue) 来维护待扩展的节点。与 BFS 按深度优先不同，Dijkstra 算法优先扩展距离起点（初始状态）累积成本 g(n) 最低的节点。

• g(n): 从初始状态 s 到当前节点 n 的实际路径成本。

算法过程概要：

1. 初始化所有节点的 g 值为无穷大，起点的 g 值为 0。将起点放入优先队列。
2. 当优先队列不为空时，取出 g 值最小的节点 n。
3. 如果 n 是目标节点，则找到了最短路径，结束。
4. 对于 n 的每个邻居 m：
   • 计算从起点经过 n 到达 m 的成本 new_g = g(n) + cost(n, m)。
   • 如果 new_g 小于当前记录的 g(m)，则更新 g(m) = new_g，并将 m 加入（或更新在）优先队列中，同时记录 n 是到达 m 的前驱节点。
5. 将 n 标记为已访问（或移入 CLOSED 列表）。

迪杰斯特拉算法的性质

• 优点：当所有边的成本（耗散值）非负时，Dijkstra 算法保证能找到从起点到所有其他可达节点的最佳解（成本最低的路径）。
• 不足：Dijkstra 算法只考虑了从起点到当前节点的已知成本 g(n)，它在选择下一个扩展节点时，没有考虑该节点距离目标节点可能还有多远。这使得它在某些情况下仍然会探索许多明显偏离目标方向的路径，导致效率不高。它是一种“向前看”不足的算法。

1.4 启发式图搜索 (Heuristic Graph Search)

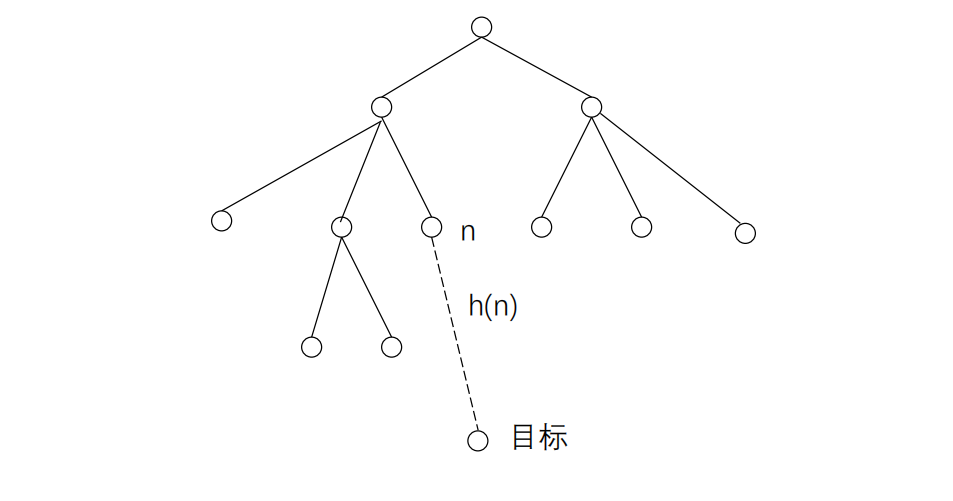
为了克服 Dijkstra 算法的不足，提高搜索效率，我们引入了启发式搜索。其核心思想是：在搜索过程中，利用与问题相关的启发信息 (Heuristic Information) 来估计从当前节点到达目标节点的“前景”或“难度”，从而引导搜索优先朝向更有希望的方向进行。

这种启发信息通常通过一个启发函数 (Heuristic Function) h(n) 来量化。

• h(n): 从当前节点 n 到目标节点 t 的估计成本。

一个好的启发函数应该能够提供有用的指引，但计算它本身的开销不能太大。启发式搜索的目标是在保证（或尽可能接近）找到最佳解的前提下，尽可能减少需要探索的状态数量（搜索范围），提高搜索效率。

1.4.1 启发式搜索算法 A (A Algorithm)

A 算法是一种经典的启发式搜索算法，它结合了 Dijkstra 算法考虑的已知成本和启发函数提供的未来成本估计。它使用一个评价函数 (Evaluation Function) f(n) 来评估节点的优先级：

f(n) = g(n) + h(n)

其中：

• f(n): 节点 n 的综合评价估计值，表示从起点经过 n 到达目标的总路径成本的估计。
• g(n): 从初始状态 s 到节点 n 的实际最小成本（与 Dijkstra 中一样）。
• h(n): 从节点 n 到目标状态 t 的估计最小成本（启发函数）。

A 算法维护两个列表：

• OPEN 表 (OPEN List)：存放已生成但尚未扩展的节点，通常实现为按 f(n) 值排序的优先队列。
• CLOSED 表 (CLOSED List)：存放已经被扩展过的节点。

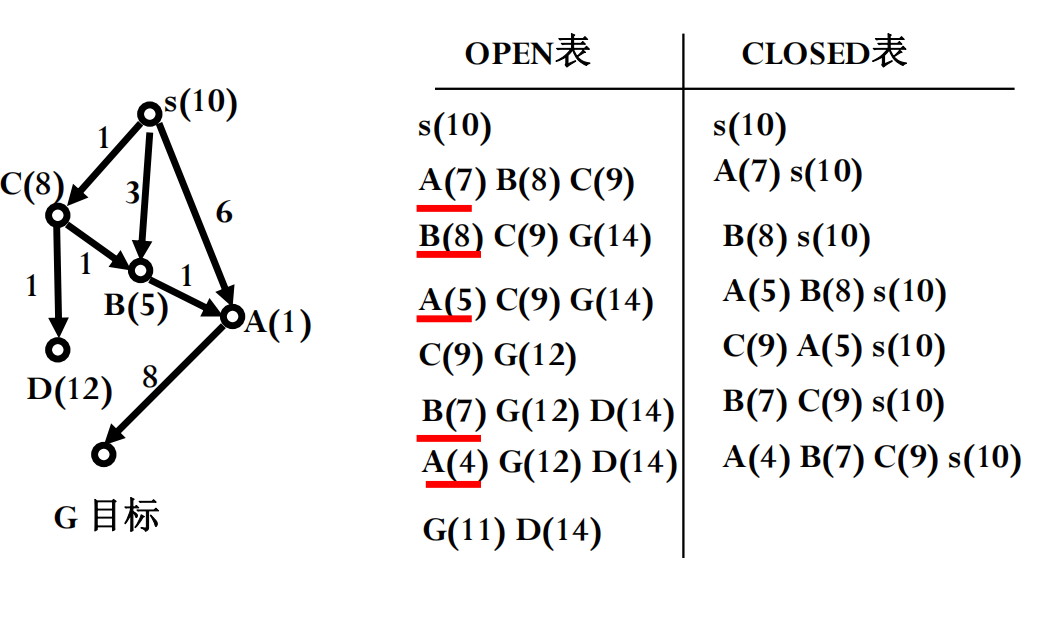
A 算法基本流程：

A-algorithm (s)   // s 为初始节点
1. 初始化 OPEN = {s}, CLOSED = {}, g(s) = 0, f(s) = g(s) + h(s)
2. while OPEN 不为空 do:
3.     从 OPEN 中取出 f(n) 值最小的节点 n
4.     if n 是目标节点 THEN return 找到路径 (通过回溯指针)
5.     将 n 从 OPEN 移除, 加入 CLOSED
6.     for 每个 n 的子节点 m do:
7.         计算 tentative_g = g(n) + cost(n, m)
8.         if m 在 CLOSED 中 and tentative_g >= g(m) then continue // 已有更好路径
9.         if m 不在 OPEN 中 or tentative_g < g(m) then // 发现新节点或更短路径
10.            设置 m 的父节点为 n
11.            设置 g(m) = tentative_g
12.            计算 f(m) = g(m) + h(m)
13.            if m 不在 OPEN 中 then 将 m 加入 OPEN
14.            else 更新 m 在 OPEN 中的值 (如果优先队列支持)
15. end while
16. return FAIL // 未找到解

符号说明： 为了更精确地讨论最优性，引入以下符号：

• g*(n): 从 s 到 n 的实际最短路径成本。
• h*(n): 从 n 到目标 t 的实际最短路径成本。
• f*(n) = g*(n) + h*(n): 从 s 经过 n 到 t 的实际最短路径成本。

我们的算法使用的是它们的估计值 g(n), h(n), f(n)。算法的目标是找到一条路径使得 f(s) = f*(s)。

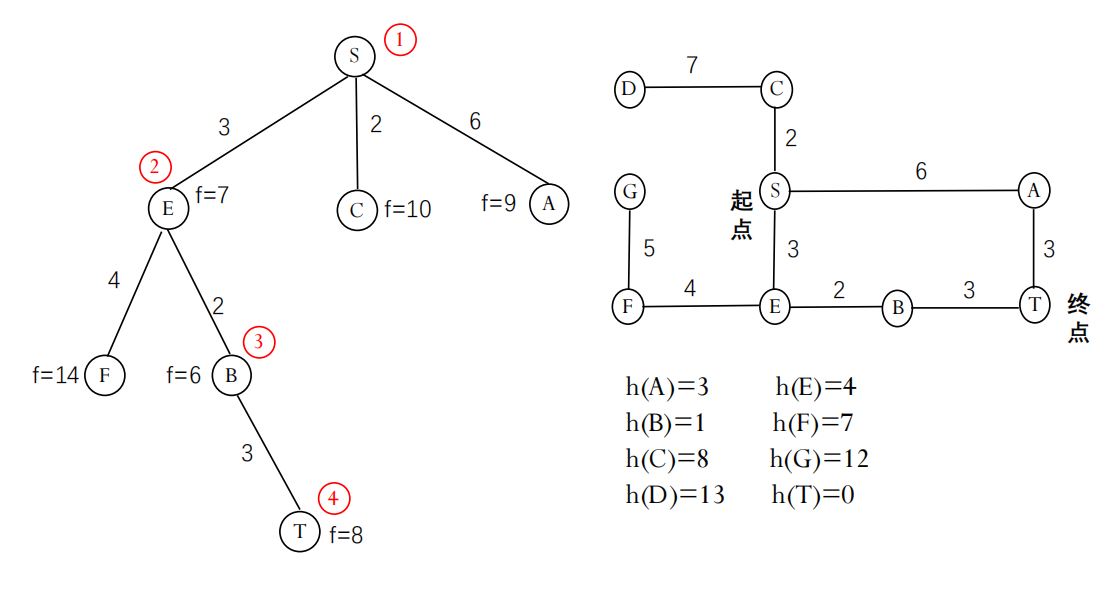
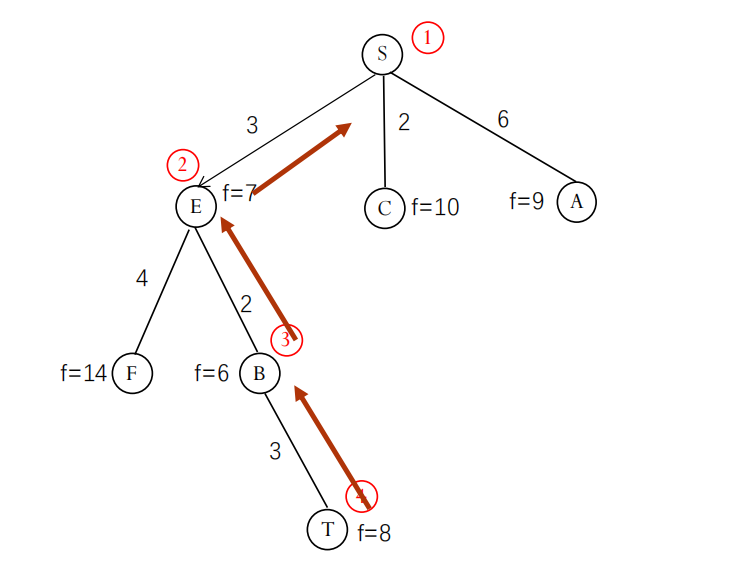
A 算法示例 (带权图)

如何得到解路径？ 当目标节点 n 被选中并确认为目标时，可以通过从 n 开始，沿着在算法过程中记录的父节点指针反向回溯，直到到达初始节点 s，即可得到从 s 到 n 的路径。

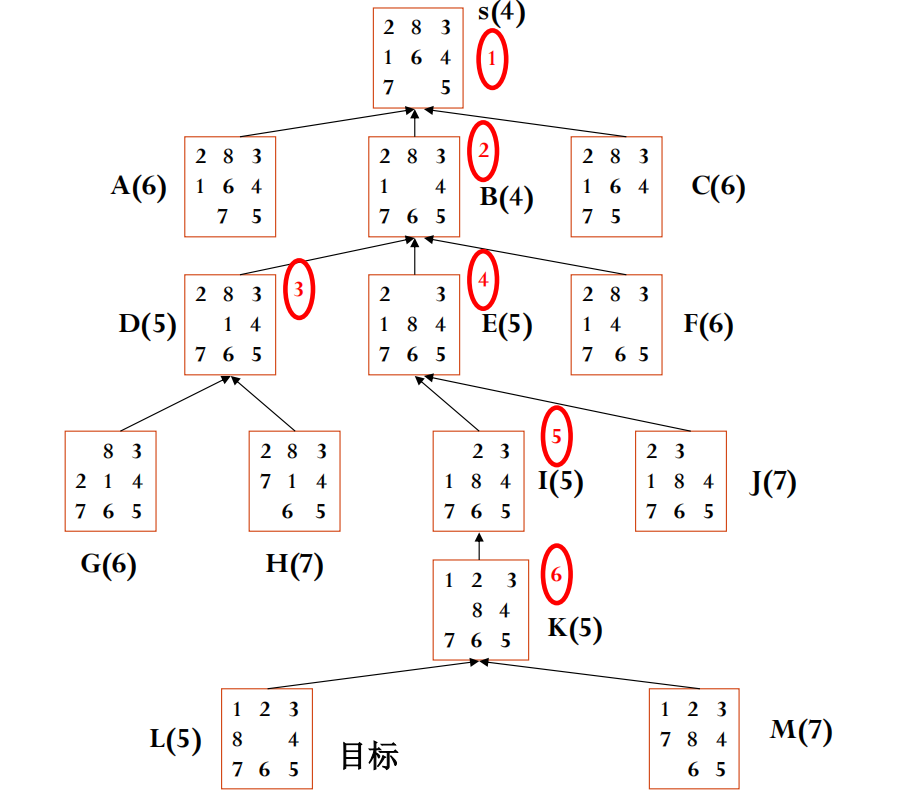
A 算法示例：八数码问题

对于八数码问题，我们可以定义：

• g(n): 从初始状态到当前状态 n 所移动的步数（假设每次移动成本为1）。
• h(n): 一个启发函数，估计从当前状态 n 到目标状态还需要的步数。

一个简单的启发函数是 “不在位的将牌数 (Number of Misplaced Tiles)”：计算当前状态下，有多少个数字（1-8）不在其目标位置上（不包括空格）。

例如，对于状态：

2 8 3
1 6 4
7   5

目标状态为：

1 2 3
8   4
7 6 5

比较可知，数字 2, 8, 1, 6 都不在目标位置（4个），只有 3, 4, 5, 7 在。所以 h(n) = 4。

假设使用 h(n) = 不在位的将牌数。A 算法会使用 f(n) = g(n) + h(n) 来指导搜索。

1.4.2 最佳图搜索算法 A* (A* Algorithm)

A 算法本身并不保证找到最优解。找到的解是否最优，取决于启发函数 h(n) 的性质。

如果启发函数 h(n) 满足 可采纳性 (Admissibility) 条件，即对于所有节点 n，h(n) 从不 overestimate 到达目标的实际最小成本 h*(n)：

\[h(n) \le h^*(n)\]

那么，使用这个可采纳启发函数的 A 算法就称为 A* 算法。

A* 算法的关键特性：

定理 (可采纳性定理)：如果存在从初始节点 s 到目标节点 t 的路径，并且使用的启发函数 h(n) 是可采纳的，则 A* 算法保证能找到最优解（成本最低的路径）并结束。

如何设计可采纳的启发函数？

一个常用的原则是放宽问题的限制条件 (Relax the problem constraints)，计算在放宽限制后的简化问题中，从当前状态到目标状态的最短路径成本。这个成本通常是原问题实际成本的一个下界，因此满足可采纳性。

示例：八数码问题的启发函数

• h1(n) = 不在位的将牌数。这个函数是可采纳的，因为每个不在位的将牌至少需要移动一次才能回到目标位置。
• h2(n) = 曼哈顿距离 (Manhattan Distance) 之和。对于每个将牌（1-8），计算它当前位置到其目标位置的水平距离和垂直距离之和，然后将所有将牌的曼哈顿距离加起来。例如，如果 ‘1’ 在 (2,1) 而目标是 (1,1)，则其曼哈顿距离是 |2-1| + |1-1| = 1。如果 ‘8’ 在 (1,2) 而目标是 (2,1)，距离是 |1-2| + |2-1| = 1+1 = 2。
  • h2(n) 也是可采纳的。因为每次移动只能使一个将牌的曼哈顿距离减少最多1（且不增加其他牌的距离），所以总距离是所需移动步数的一个下界。
  • 通常，$h2(n) \ge h1(n)$ (目标节点除外)。例如，一个牌离目标位置很远但恰好占了另一个牌的目标位置，h1 只算1次不在位，h2 会计算较长的距离。

示例：传教士与野人问题的启发函数

假设有 M 个传教士和 C 个野人在起始岸（左岸），目标是将他们全部运到对岸（右岸），船容量为 K。

放宽约束：忽略“野人不能吃传教士”的规则。

问题变为：最少需要多少次单程渡河才能把左岸的 M_L + C_L 人全部运到右岸？

每次船最多运 K 人过去。如果忽略返回（或者假设有无数小船可以单程运），那么至少需要 $\lceil (M_L + C_L) / K \rceil$ 次单程。这个值就是 h(n) 的一个简单可采纳估计。

启发函数的优劣比较

如果对于同一个问题，有两个可采纳的启发函数 h1(n) 和 h2(n)，并且对于所有非目标节点 n，都有 h2(n) > h1(n)，那么我们称 h2 比 h1 更具有信息量 (more informed)。

定理 (启发函数优势定理)：如果 A* 算法使用 h2 扩展的每一个节点也必定会被使用 h1 的 A* 算法所扩展（假设都找到了最优路径）。换句话说，更具信息量的启发函数（h2）通常会导致 A* 扩展更少的节点。

评价启发函数效果：有效分支因子 (Effective Branching Factor, b*)

一个衡量启发函数好坏的实验指标是有效分支因子 b*。如果 A* 算法找到深度为 d 的解时总共扩展了 N 个节点，那么 b* 定义为满足以下方程的数：

\[N = 1 + b^* + (b^*)^2 + \dots + (b^*)^d\]

b* 越接近 1，说明启发函数越有效，搜索越集中。实验表明，对于同一问题，b* 通常相对稳定，不随问题规模剧烈变化。

示例：八数码问题的 b*

• 使用 h1 (不在位牌数): $d=14, N=539 \implies b^*=1.44$; $d=20, N=7276 \implies b^*=1.47$
• 使用 h2 (曼哈顿距离): $d=14, N=113 \implies b^*=1.23$; $d=20, N=676 \implies b^*=1.27$

可见，h2 确实更有效，导致扩展的节点数显著减少，b* 更小。

练习题

对于8数码问题，假设移动一个将牌的耗散值为该将牌上的数字（例如，移动数字’3’的成本是3）。请思考如何使用A*算法求解该问题，并尝试手工演算一个简单例子或编程实现。你需要重新定义 g(n)（路径成本是移动将牌数字之和）并选择一个可采纳的 h(n)（例如，曼哈顿距离仍然可采纳，因为它仍然是移动次数的下界，而移动成本非负）。

1.4.3 A* 算法的改进：单调性与修正 A*

问题的提出：

标准的 A/A* 算法在某些情况下可能会重复扩展同一个节点。这发生在算法第一次找到到达节点 n 的路径时，该路径不是最优的 (g(n) > g*(n))。后来，算法通过另一条路径以更低的成本 g'(n) < g(n) 再次到达 n。如果此时 n 已经在 CLOSED 表中，标准 A 算法可能需要将其重新放回 OPEN 表（或者更新其 g 值并重新考虑），这可能导致 n 被多次扩展，降低效率。

解决途径：

1. 对启发函数 h 加以更强的限制：引入单调性 (Monotonicity) 或 一致性 (Consistency) 条件。
2. 对算法本身加以改进：设计避免或减少节点多次扩展的算法变体。

单调性 (Monotonicity / Consistency)

一个启发函数 h 被称为是单调的 (Monotonic) 或 一致的 (Consistent)，如果对于任意节点 n 和它的任一子节点 m（通过动作 a 到达，成本为 c(n, m)），满足以下条件 (三角形不等式)：

$h(n) \le c(n, m) + h(m)$

并且，对于所有目标节点 t，h(t) = 0。

直观理解：从 n 到目标的估计成本，不应该大于 从n走一步到m的成本 加上 从m到目标的估计成本。

单调性的重要性质：

定理：如果启发函数 h(n) 是单调的，那么当 A* 算法选择节点 n 进行扩展时，它已经找到了到达节点 n 的最佳路径。即，此时有 g(n) = g*(n)。

推论：如果 h 是单调的，A* 算法扩展的任何节点都不需要被重新扩展。当一个节点被放入 CLOSED 表时，算法已经找到了通往该节点的最优路径。

单调性与可采纳性的关系：

可以证明，任何单调的启发函数都一定是可采纳的。（可以通过从目标节点 t (满足 $h(t)=0 \le h*(t)=0$) 向父节点进行数学归纳来证明）。反之不一定成立，可采纳的 h 不一定是单调的。

示例：八数码问题的 h 单调性

• h1(n) = 不在位将牌数：假设移动成本 c(n,m) = 1。移动一个牌，h 值变化量 h(n) - h(m) 只能是 -1, 0, 或 1。由于 c(n, m) = 1，条件 $h(n) - h(m) \le c(n, m)$ 总是满足。且 h(goal) = 0。因此 h1 是单调的。
• h2(n) = 曼哈顿距离和：同样可以证明 h2 也是单调的（当移动成本为1时）。

使用单调启发函数可以简化 A* 算法的实现（无需处理 CLOSED 表中节点的更新问题），并保证效率。

改进算法：修正的 A* 算法 (Modified A*)

即使 h 不是单调的，也可以通过修改算法来尝试减少重复扩展。一种思路是利用已找到的最优解成本的信息（或其估计）。

设 f*(s) 为从起点到目标的实际最优路径成本。有以下结论：

• OPEN 表上任何具有 f(n) < f*(s) 的节点最终一定会被 A* 扩展。
• A* 选作扩展的任一节点 n，必有 $f(n) \le f*(s)$。

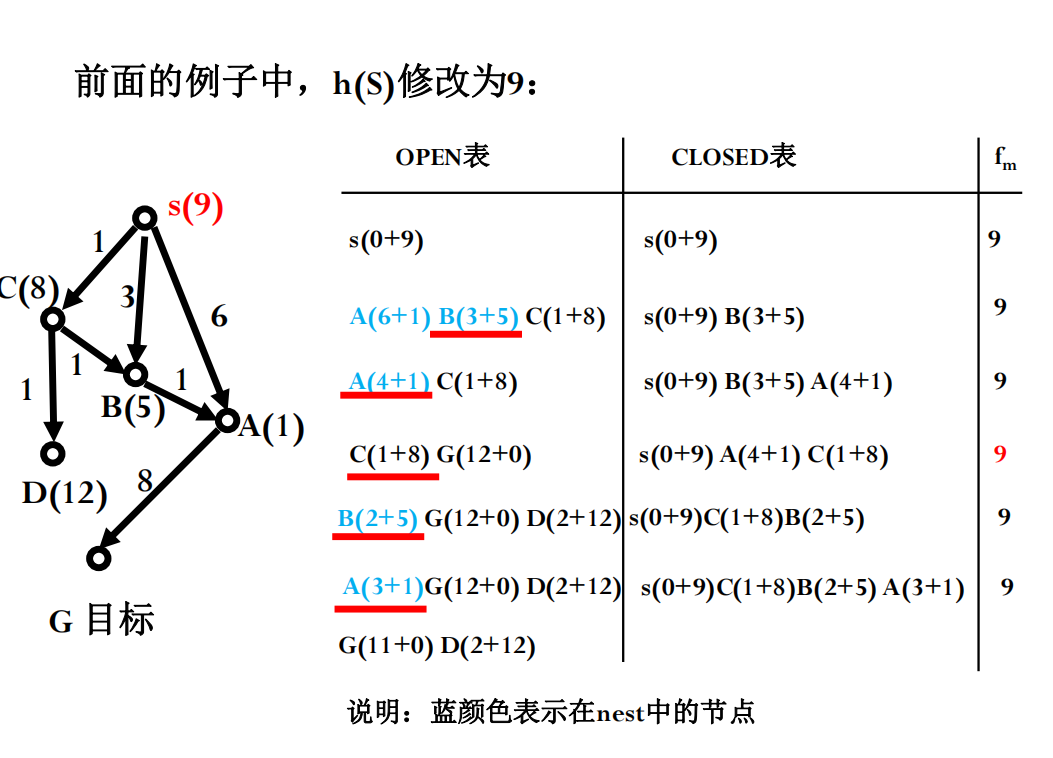
修正的 A* 算法引入一个变量 fm，记录到目前为止已扩展节点的最大 f 值。它优先考虑 OPEN 表中那些 f 值严格小于 fm 的节点（称这些节点集合为 NEST），认为它们更有可能位于比当前已知最好路径（其成本上限由 fm 反映）还要好的路径上。在 NEST 中，选择 g 值最小的节点扩展（倾向于选择靠近起点的）。如果 NEST 为空，则从整个 OPEN 表中选择 f 最小的节点 n，并更新 fm = f(n)。

Modified-A-Star-Algorithm(s) // s is the initial node
1. Initialize OPEN = {s} (as a priority queue ordered by f-value)
2. Initialize CLOSED = {} (as a set of visited nodes)
3. Initialize g(s) = 0
4. Calculate f(s) = g(s) + h(s)
5. Initialize fm = 0 // Stores the maximum f-value among expanded nodes so far

6. while OPEN is not empty do:
7.     // --- Node Selection ---
8.     NEST = {ni | ni ∈ OPEN and f(ni) < fm} // Find nodes with f-value strictly less than fm

9.     if NEST is not empty then
10.        // Select the node with the minimum g-value from NEST
11.        n = node in NEST with the minimum g(n) value
12.    else
13.        // Select the node with the minimum f-value from the entire OPEN list
14.        n = node in OPEN with the minimum f(n) value
15.        fm = f(n) // Update fm as we are expanding based on the overall minimum f-value
16.
17.    // --- Goal Check ---
18.    if n is a goal node THEN
19.        return the path reconstructed by tracing back parents from n to s
20.
21.    // --- Expansion Preparation ---
22.    Remove n from OPEN
23.    Add n to CLOSED
24.
25.    // --- Successor Processing ---
26.    for each successor m of n do:
27.        // Calculate tentative cost to reach m through n
28.        tentative_g = g(n) + cost(n, m)
29.
30.        // --- Check against CLOSED list ---
31.        if m ∈ CLOSED and tentative_g >= g(m) then
32.            // A path to m through n is not better than the one already found and expanded
33.            continue // Skip processing this successor
34.        else if m ∈ CLOSED and tentative_g < g(m) then
35.            // Found a better path to a node already expanded!
36.            Remove m from CLOSED // It needs to be reconsidered and potentially re-expanded
37.            // Let it fall through to the OPEN list check/addition below
38.
39.        // --- Check against OPEN list ---
40.        if m ∈ OPEN and tentative_g >= g(m) then
41.            // A path to m through n is not better than the existing path in OPEN
42.            continue // Skip processing this successor
43.        else if m ∈ OPEN and tentative_g < g(m) then
44.            // Found a better path to a node already in OPEN
45.            Set parent of m to n
46.            g(m) = tentative_g
47.            f(m) = g(m) + h(m)
48.            // Update m's priority in OPEN (decrease-key operation in priority queue)
49.        else if m ∉ OPEN then // (and m is not in CLOSED anymore, due to step 36)
50.            // Discovered a completely new node or found the first path to a node previously in CLOSED
51.            Set parent of m to n
52.            g(m) = tentative_g
53.            f(m) = g(m) + h(m)
54.            Add m to OPEN
55.
56. end while // End of main loop
57.
58. // If OPEN becomes empty and goal was not reached
59. return FAIL // No solution found

思考题总结:

• 算法关系: BFS 是 A* 在 g(n) 为层数且 h(n)=0 时的特例。Dijkstra 是 A* 在 h(n)=0 时的特例（处理非负权图）。A 是 A* 的一般形式（不要求 h 可采纳）。
• 寻找前 N 个解: 需要修改算法，允许一个节点被多次放入 OPEN 表（如果通过不同路径到达），并在 OPEN/CLOSED 表中为每个节点保留（最多）N 条到达它的最佳路径及其成本。当找到一个目标时记录下来，并继续搜索直到找到 N 个或 OPEN 表为空。

1.5 其他搜索算法简介

除了上述基于图搜索的经典算法外，还有其他类型的搜索方法：

• 爬山法 (Hill Climbing)：一种局部搜索 (Local Search) 算法。它不维护搜索树，只保留当前状态，并尝试移动到邻居状态中“最好”（根据某个评价函数，通常类似启发函数）的那一个。容易陷入局部最优 (Local Optima) 而非全局最优。
• 随机搜索算法 (Randomized Search)：如模拟退火 (Simulated Annealing), 遗传算法 (Genetic Algorithms) 等，它们引入随机性来跳出局部最优，探索更广阔的搜索空间。
• 动态规划 (Dynamic Programming, DP)：适用于具有最优子结构 (Optimal Substructure) 和重叠子问题 (Overlapping Subproblems) 的问题。它通过存储子问题的解来避免重复计算。

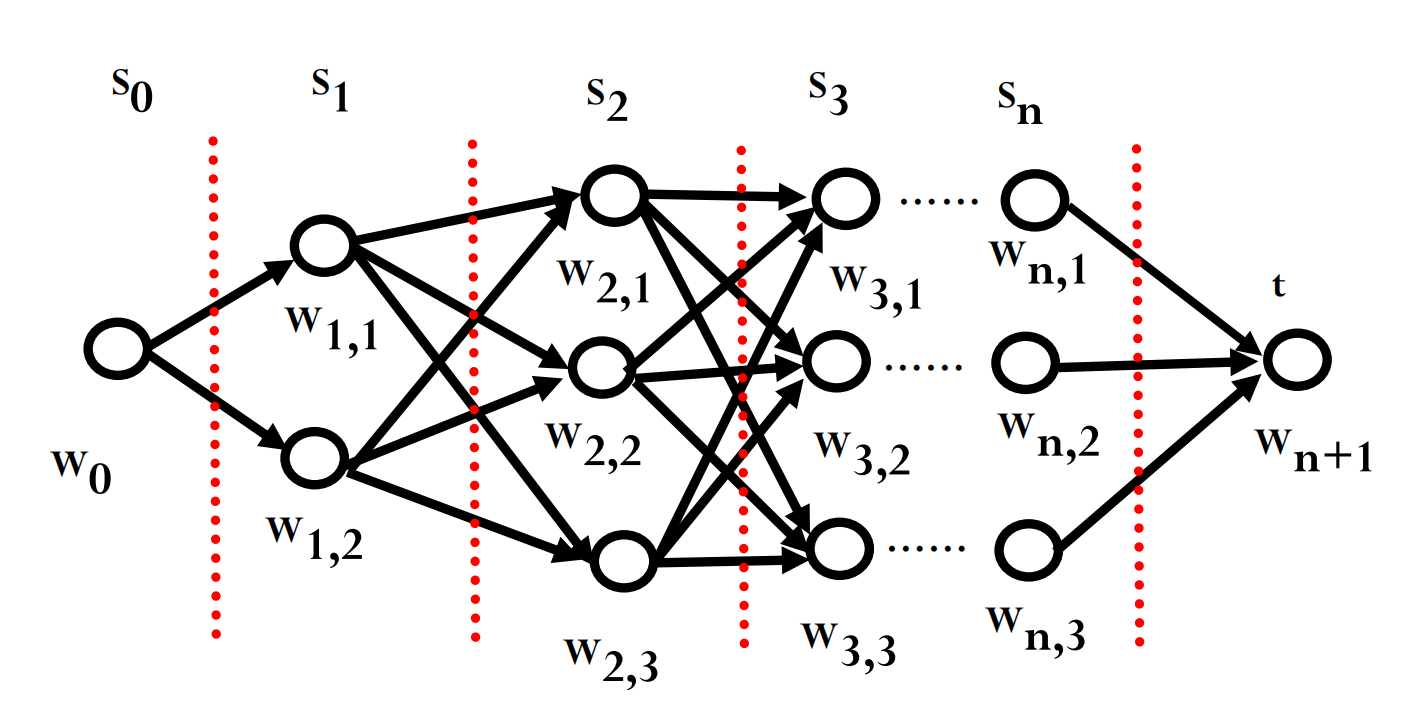
  • Viterbi 算法 是一个典型的 DP 算法，常用于寻找序列数据（如时间序列、文本序列）中最可能的隐藏状态序列。例如，在给定观测序列（如语音信号或拼音串）时，找到最可能的词序列。Viterbi 算法可以看作是在一个特定的图结构（称为格 trellis）上寻找最短路径的问题。 设 Q(Wi,j) 是到达第 i 阶段第 j 个状态的最佳路径值（例如，最小成本或最大概率），D(Wi-1,k, Wi,j) 是从前一阶段状态 k 转移到当前阶段状态 j 的成本（或概率的负对数）。Viterbi 的递推公式通常形如：

    \[Q(W_{i,j}) = \min_{k} \{ Q(W_{i-1,k}) + D(W_{i-1,k}, W_{i,j}) \} \quad (i > 0)\] \[Q(W_{0,j}) = \text{initial cost/prob for state } j\]

    这与图搜索中更新节点成本 g(n) 的思想类似。

    

1.6 搜索算法实用举例

搜索算法，特别是基于最短路径思想的算法（如 Dijkstra, A*, Viterbi），在许多实际应用中发挥着关键作用。

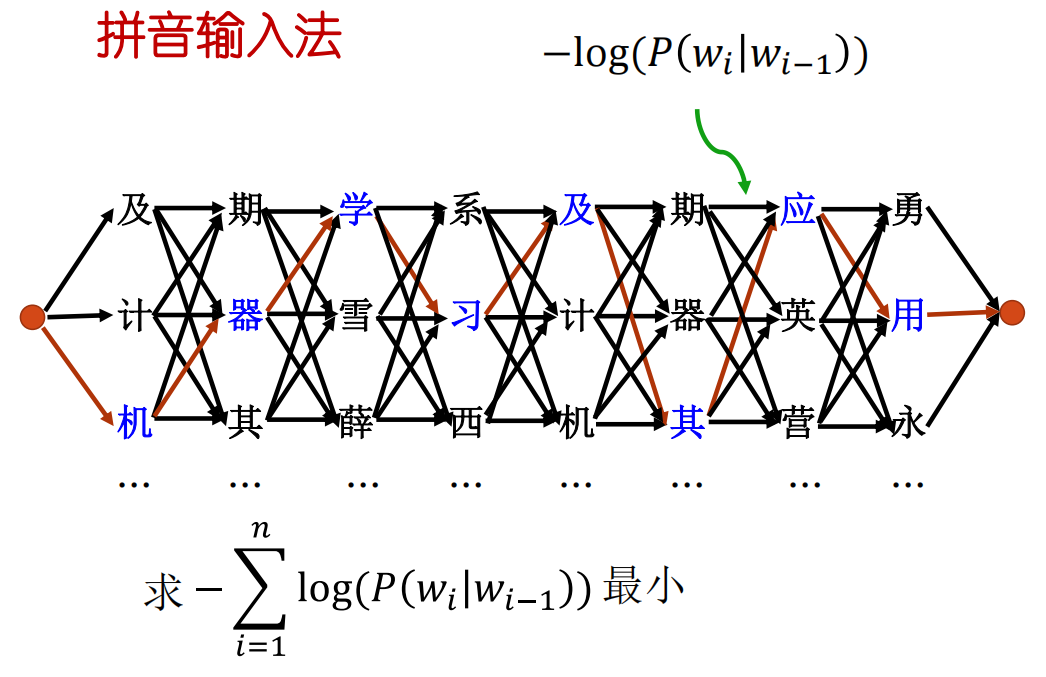
拼音输入法 (Pinyin Input Method Editor, IME)

当用户输入一串拼音时（如 “jiqixuexi”），输入法需要将其转换为最可能的汉字序列（如 “机器学习”）。

• 问题：给定一个拼音观测序列 O = o1 o2 ... on，找到最可能的汉字词序列 S = w1 w2 ... wn。
• 建模：使用贝叶斯定理，我们想最大化后验概率 $P(S|O) = \frac{P(O|S) P(S)}{P(O)}$。由于 $P(O)$ 对所有候选序列 S 都是常量，问题变为最大化 $P(O|S) P(S)$。
  • $P(O|S)$ 是声学/输入模型（给定汉字序列，用户输入对应拼音的概率），通常简化处理或认为近似为1。
  • $P(S)$ 是语言模型 (Language Model)，表示汉字序列 S 自身出现的概率。常用的语言模型是 N-gram 模型，例如 二元语法 (Bigram Model)： $P(S) = P(w_1) P(w_2|w_1) P(w_3|w_2) \dots P(w_n|w_{n-1}) = \prod_{i=1}^{n} P(w_i|w_{i-1})$ (约定 $w_0$ 是句子开始符)
• 求解：最大化 $\prod P(w_i|w_{i-1})$ 等价于最小化 $\sum -\log P(w_i|w_{i-1})$。
  • 构建一个格状图 (Trellis)：
    • 每个阶段 i 对应拼音 oi。
    • 每个阶段的节点对应于拼音 oi 可能的汉字 wi。
    • 从阶段 i-1 的节点 w_{i-1} 到阶段 i 的节点 wi 的边，其权重（成本）设为 $-\log P(w_i|w_{i-1})$。
  • 在这个图上寻找从起点（句子开始）到终点（句子结束）的最短路径。这条路径对应的汉字序列就是最可能的句子。
  • Viterbi 算法 正是用于高效解决这个最短路径问题的动态规划算法。

  

  汉语中一个拼音平均对应10个汉字，一个11个音的句子可能有 $10^{11}$ 种组合，暴力枚举不可行。Viterbi 算法的复杂度大致与 (句子长度) * (每个拼音的候选汉字数)^2 成正比，远低于指数级。

汉字识别后处理 (OCR Post-processing)

光学字符识别 (OCR) 系统将图像中的文字转换为文本，但可能产生错误。例如，把“我们”识别成“优仍”。后处理的目标是利用语言知识修正这些错误。

• 问题：给定一个 OCR 输出的候选字符序列（可能每个位置有多个候选字符及其置信度），找到最符合语言习惯且与识别结果最接近的真实文本序列。
• 建模：类似于 IME，也需要结合识别置信度和语言模型。假设 OCR 为每个位置 i 的候选字符 wi 给出一个识别信度 CF(wi) (Confidence)。我们想找到序列 S = w1...wn 来最大化类似 $\prod_{i=1}^{n} [CF(w_i) \times P(w_i|w_{i-1})]$ 的得分（这里简化了模型）。
• 求解：同样可以转换为在格状图上寻找最佳路径的问题。边的权重可以基于识别信度和转移概率（例如，$-\log(CF(w_i)) - \log(P(w_i|w_{i-1}))$）。Viterbi 算法再次适用。

概率计算与平滑

语言模型概率 $P(w_i|w_{i-1})$ 通常从大规模文本语料库中统计得到： $P(w_i|w_{i-1}) = \frac{\text{count}(w_{i-1}w_i)}{\text{count}(w_{i-1})}$ 可能会遇到数据稀疏问题（某些词对从未出现过，导致概率为0）。需要使用平滑 (Smoothing) 技术，如加一平滑、Good-Turing 平滑或插值平滑（如幻灯片94所示）： $P_{smoothed}(w_i|w_{i-1}) = \lambda P(w_i|w_{i-1}) + (1-\lambda) P(w_i)$ 将低阶 N-gram (如 unigram $P(w_i)$) 的信息插值进来，避免零概率。

小结

本章我们探讨了搜索问题的基本概念和框架，主要介绍了两类搜索策略：

• 盲目搜索：不利用问题特定知识。
  • 深度优先搜索 (DFS)：深入探索，内存高效，但不保证最优，可能不完备（需控制）。
  • 宽度优先搜索 (BFS)：逐层探索，保证找到最短（单位成本）路径，完备，但空间复杂度高。
• 启发式搜索：利用启发函数 h(n) 指导搜索。
  • Dijkstra 算法：基于实际成本 g(n)，找到最优路径（非负权），但未利用启发信息。
  • A 算法：结合 g(n) 和 h(n)，使用 f(n) = g(n) + h(n) 评估节点。
  • A* 算法：A 算法的一种，当 h(n) 可采纳 (h(n) <= h*(n)) 时，保证找到最优解。启发函数的设计（如松弛约束）和质量（如单调性、信息量 b*）对效率至关重要。
  • 改进的 A* 算法：通过利用单调性或修改算法（如修正 A*）来提高效率，减少节点重扩展。
• 动态规划：适用于有最优子结构和重叠子问题的问题，如 Viterbi 算法，常用于序列数据的最短路径/最可能序列查找，在拼音输入法、OCR 后处理等领域有广泛应用。

理解这些搜索算法的原理、特性、优缺点以及它们之间的关系，对于解决计算机科学和人工智能中的许多问题至关重要。