Sorting - Quick Sort

基本原理

快速排序的核心思想是通过分治来实现排序。其中最关键的步骤是选取和培养轴点(pivot)。

轴点的特性

轴点需满足以下条件：

• max[Lo,mi) ≤ [mi] ≤ min(mi,hi)
• 即轴点左侧的所有元素不大于轴点
• 轴点右侧的所有元素不小于轴点

排序过程

1. 选取并培养轴点
2. 将序列分为左右两个子序列
3. 对子序列递归执行快速排序

\[sorted(S) = sorted(S左) + pivot + sorted(S右)\]

template <typename T> //向量快速排序
void Vector<T>::quickSort( Rank lo, Rank hi ) { // 0 <= lo < hi <= size
   if ( hi - lo < 2 ) return; //单元素区间自然有序，否则...
   Rank mi = partition( lo, hi ); //在[lo, hi)内构造轴点
   quickSort( lo, mi ); quickSort( mi + 1, hi ); //前缀、后缀各自递归排序
}

轴点的性质

• 必要条件：轴点必定已然就位（尽管反之不然）
• 充分条件：一个序列有序，当且仅当所有元素皆为轴点
• 快速排序本质：就是将所有元素逐个转换为轴点的过程
• 坏消息：一个序列中未必总有轴点，这种情况称为”derangement”（错位排列）
  • 例如：顺序序列经过循环移位后的状态
• 好消息：通过少量交换操作，即可使任一元素转为轴点

待解决问题

• 如何进行元素交换？
• 交换操作的成本是多少？

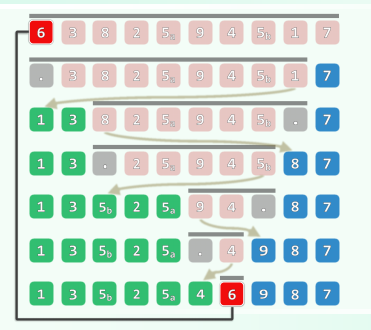
快速划分：LUG版

减而治之，相向而行

1. 选择候选轴点
   • 选取第一个元素 A[0] 作为候选轴点
2. 划分过程
   • 将序列分为三个部分：L(Less) + U(Unknown) + G(Greater)
   • 使用双指针 lo 和 hi 从两端向中间移动
   • 检查过程：
     • 若当前元素小于轴点：归入 L 区
     • 若当前元素大于轴点：归入 G 区
3. 轴点确定
   • 当 lo == hi 时，将候选轴点放置在 L 和 G 的分界处
4. 性能分析
   • 时间复杂度：O(n)
     • 普通元素最多移动一次
     • 轴点元素最多移动两次
   • 空间复杂度：O(1)
     • 仅需常数额外空间

template <typename T> //通过调整元素位置，构造出区间[lo, hi)内的一个轴点
Rank Vector<T>::partition( Rank lo, Rank hi ) { // LUG版：基本形式
   swap( _elem[lo], _elem[lo + rand() % ( hi - lo )] ); //任选一个元素与首元素交换
   T pivot = _elem[lo]; //经以上交换，等效于随机选取候选轴点
   while ( lo < hi ) { //从两端交替扫描，直至相遇
      do hi--; while ( ( lo < hi ) && ( pivot <= _elem[hi] ) ); //向左拓展后缀G
      if ( lo < hi ) _elem[lo] = _elem[hi]; //阻挡者归入前缀L
      do lo++; while ( ( lo < hi ) && ( _elem[lo] <= pivot ) ); //向右拓展前缀L
      if ( lo < hi ) _elem[hi] = _elem[lo]; //阻挡者归入后缀G
   } //assert: quit with lo == hi or hi + 1
   _elem[hi] = pivot; //候选轴点置于前缀、后缀之间，它便名副其实
   return hi; //返回轴点的秩
}

不变性：L = [0,lo)；U = (lo,hi)；G = [hi,n)；[lo] == [hi]

性能特征

• 线性时间
  • 尽管lo、hi交替移动
  • 累计移动距离不过O(n)
• 就地算法(in-place)
  • 只需O(1)附加空间
• 不稳定性(unstable)
  • lo/hi的移动方向相反
  • 相等的元素可能前后颠倒

迭代、贪心与随机

空间复杂度分析

空间复杂度与递归深度相关：

• 最好情况：划分总是均衡，O(logn)
• 最差情况：划分总是偏向一侧，O(n)
• 平均情况：保持相对均衡，O(logn)

优化思路

关键问题：如何避免最坏情况？ 解决方案：迭代化 + 贪心策略

#define Put( K, s, t ) { if ( 1 < (t) - (s) ) { K.push(s); K.push(t); } }
#define Get( K, s, t ) { t = K.pop(); s = K.pop(); }

template <typename T> //向量快速排序
void Vector<T>::quickSort( Rank lo, Rank hi ) { //0 <= lo < hi <= size
   Stack<Rank> Task; Put( Task, lo, hi ); //类似于对递归树的先序遍历
   while ( !Task.empty() ) {
      Get( Task, lo, hi );
      Rank mi = partition( lo, hi ); //在[lo, hi)内构造轴点
      if ( mi - lo < hi - mi ) { Put( Task, mi+1, hi ); Put( Task, lo, mi ); }
      else                     { Put( Task, lo, mi ); Put( Task, mi+1, hi ); }
   } //大任务优先入栈（小任务优先出栈执行），可保证递归深度（空间成本）不过O(logn)
}

空间复杂度分析 O(logn)

通过归纳法证明：

1. 归纳假设：对长度 m < n 的序列，算法所需空间不超过 log m
2. 考查长度为 n 的序列，算法执行过程分为三个阶段：

第一阶段：初始划分

• 经过第一次迭代(划分)后， $ \vert Task \vert $ = 2
• 栈顶子任务 V 必是轻的： $ \vert V \vert $ = v ≤ [n/2]
• 栈底子任务 U 必有削减： $ \vert U \vert $ = u ≤ n-1 < n

第二阶段：处理 V

在对 V 的排序(共 v 次划分)过程中，根据归纳假设：

• 所需空间量 ≤ 1 + log v ≤ 1 + log(n/2) = log n

第三阶段：处理 U

在对 U 的排序(共 u 次划分)过程中，根据归纳假设：

• 所需空间量 ≤ log u < log n

时间复杂度分析

最好情况

• 每次划分都(接近)平均，轴点总是(接近)中央
• T(n) = 2·T((n-1)/2) + O(n) = O(n·log n)
• 达到理论下界！

最坏情况

• 每次划分都极不均衡（如轴点总是最小/大元素）
• T(n) = T(n-1) + T(0) + O(n) = O(n²)
• 性能退化至与冒泡排序相当

注：虽然采用随机选取(Randomization)、三者取中(Sampling)等策略可以降低最坏情况的概率，但无法完全避免。

递归深度

居中 + 偏侧：三者取中

• 好轴点：落在宽度为 $ \lambda \cdot n $ 的居中区间
• 坏轴点：落在两侧(概率为 $ 1-\lambda $ )

若采用三者取中策略，以 $ \lambda=0.5 $ 为例，好轴点的概率为：

\[1 \times 0.50 \times 0.50 \times 0.50 + 3 \times 0.50 \times 0.50 \times 0.25 + 3 \times 0.25 \times 0.50 \times 0.50 + 6 \times 0.25 \times 0.50 \times 0.25 = 68.75\%\]

递归深度：常规随机

• 最坏情况递归 $ \Omega(n) $ 层，概率极低
• 平均情况递归 $ O(\log n) $ 层，概率极高

实际上：除非过于侧偏的 pivot，都会有效地缩短递归深度

断言 1：在任何一条递归路径上，好轴点绝不会多于：

\[d(n,A)=\log_{2/(1+x)}n\]

断言 2：抵达 $ \frac{1}{\lambda} \cdot d(n,X) $ 层时，即可期望地出现 $ d(n,\lambda) $ 个好轴点——从而在此之前终止

递归深度：以 $ \lambda=0.5 $ 估计

\[d(n,1/2)=\log_{4/3}n \approx 2.41 \cdot \log n\]

断言：任何一条递归路径的长度，只有极小的概率超过：

\[D(n,1/2)=\frac{2}{\lambda} \cdot d(n,1/2) \approx 9.64 \cdot \log_2 n\]

事实上，此概率：

\[\begin{aligned} & \leq \sum_{i=0}^{d}\binom{D}{i} \cdot \lambda^i \cdot (1-\lambda)^{D-i} = 2^{-D} \cdot \sum_{i=0}^{d}\binom{D}{i} \\ & \leq 2^{-4d} \cdot (eD/d)^d \quad (\because \sum_{i=0}^{k}\binom{N}{i} \leq (eN/k)^k) \\ & = 16^{-d} \cdot (4e)^d = (e/4)^{\log_{4/3}n} = n^{\log_{4/3}e/4} \approx n^{-1.343} \end{aligned}\]

当 $ n=10^6 $ 时，递归深度不超过 D 的概率 $ \geq 1-n^{-0.343} > 99.1223\% $

比较次数

递推分析

• 记期望的比较次数为 $ T(n) $ : $ T(1)=0 $ , $ T(2)=1 $ , …
• 可以证明: $ T(n)=\mathcal{O}(n \log n) $ …

\[\begin{aligned} T(n) &= (n-1)+\frac{1}{n} \cdot \sum_{k=0}^{n-1}[T(k)+T(n-k-1)] \\ &= (n-1)+\frac{2}{n} \cdot \sum_{k=0}^{n-1} T(k) \\ n \cdot T(n) &= n \cdot(n-1)+2 \times \sum_{k=0}^{n-1} T(k) \\ (n-1) \cdot T(n-1) &= (n-1) \cdot(n-2)+2 \times \sum_{k=0}^{n-2} T(k) \end{aligned}\] \[\begin{aligned} n \cdot T(n)-(n-1) \cdot T(n-1) &= 2 \cdot(n-1)+2 \times T(n-1) \\ n \cdot T(n)-(n+1) \cdot T(n-1) &= 2 \cdot(n-1) \end{aligned}\] \[\frac{T(n)}{n+1}-\frac{T(n-1)}{n}=\frac{4}{n+1}-\frac{2}{n}\] \[\frac{T(n)}{n+1}=\frac{T(n)}{n+1}-\frac{T(1)}{2}=4 \cdot \sum_{k=2}^{n} \frac{1}{k+1}-2 \cdot \sum_{k=2}^{n} \frac{1}{k}=2 \cdot \sum_{k=1}^{n+1} \frac{1}{k}+\frac{2}{n+1}-4 \approx 2 \cdot \ln n\] \[T(n) \approx 2 \cdot n \cdot \ln n=(2 \cdot \ln 2) \cdot n \log n \approx 1.386 \cdot n \log n\]

后向分析

设经排序后得到的输出序列为： $ {a_0,a_1,a_2,\ldots,a_i,\ldots,a_j,\ldots,a_{n-1}} $

这一输出与具体使用何种算法无关，故可使用后向分析。比较操作的期望次数应为：

\[T(n)=\sum_{i=0}^{n-2} \sum_{j=i+1}^{n-1} \operatorname{Pr}(i, j)=\sum_{j=1}^{n-1} \sum_{i=0}^{j-1} \operatorname{Pr}(i, j)\]

亦即，每一对 $ (a_i,a_j) $ 在排序过程中会做比较之概率的总和。

quickSort的过程及结果可理解为：将所有元素逐个地转化为pivot。若 $ k \notin [i,j] $ ，则 $ a_k $ 早于或晚于 $ a_i $ 和 $ a_j $ 被转化，均与 $ \operatorname{Pr}(i,j) $ 无关。

进一步地， $ (a_i,a_j) $ 会做比较，当且仅当在 $ {a_i,a_{i+1},a_{i+2},\ldots,a_{j-2},a_{j-1},a_j} $ 中， $ a_i $ 或 $ a_j $ 率先被转化。

\[T(n)=\sum_{j=1}^{n-1} \sum_{i=0}^{j-1} \operatorname{Pr}(i, j)=\sum_{j=1}^{n-1} \sum_{d=1}^{j} \frac{2}{d+1} \approx \sum_{j=1}^{n-1} 2 \cdot(\ln j-1) \leq 2 \cdot n \cdot \ln n\]

快速划分：DUP版

处理相等元素的问题

当序列中存在大量与轴点相等的元素时，会出现以下问题：

• 切分点会接近于 lo
• 导致划分极度失衡
• 递归深度接近 O(n)
• 运行时间退化至接近 O(n²)

这种情况的尴尬之处在于：当所有元素都相等时，实际上根本无需排序。通过对 LUG 版本进行简单调整即可解决这个问题。

LUG 版本（原始）

template <typename T> //通过调整元素位置，构造出区间[lo, hi)内的一个轴点
Rank Vector<T>::partition( Rank lo, Rank hi ) { // LUG版：基本形式
   swap( _elem[lo], _elem[lo + rand() % ( hi - lo )] ); //任选一个元素与首元素交换
   T pivot = _elem[lo]; //经以上交换，等效于随机选取候选轴点
   while ( lo < hi ) { //从两端交替扫描，直至相遇
      do hi--; while ( ( lo < hi ) && ( pivot <= _elem[hi] ) ); //向左拓展后缀G
      if ( lo < hi ) _elem[lo] = _elem[hi]; //阻挡者归入前缀L
      do lo++; while ( ( lo < hi ) && ( _elem[lo] <= pivot ) ); //向右拓展前缀L
      if ( lo < hi ) _elem[hi] = _elem[lo]; //阻挡者归入后缀G
   } //assert: quit with lo == hi or hi + 1
   _elem[hi] = pivot; //候选轴点置于前缀、后缀之间，它便名副其实
   return hi; //返回轴点的秩
}

快速划分：DUP版

template <typename T> //通过调整元素位置，构造出区间[lo, hi)内的一个轴点
Rank Vector<T>::partition( Rank lo, Rank hi ) { // DUP版：可优化处理多个关键码雷同的退化情况
   swap( _elem[lo], _elem[lo + rand() % ( hi - lo )] ); //任选一个元素与首元素交换
   T pivot = _elem[lo]; //经以上交换，等效于随机选取候选轴点
   while ( lo < hi ) { //从两端交替扫描，直至相遇
      do hi--; while ( ( lo < hi ) && ( pivot <  _elem[hi] ) ); //向左拓展后缀G
      if ( lo < hi ) _elem[lo] = _elem[hi]; //阻挡者归入前缀L
      do lo++; while ( ( lo < hi ) && ( _elem[lo] <  pivot ) ); //向右拓展前缀L
      if ( lo < hi ) _elem[hi] = _elem[lo]; //阻挡者归入后缀G
   } //assert: quit with lo == hi or hi + 1
   _elem[hi] = pivot; //候选轴点置于前缀、后缀之间，它便名副其实
   return hi; //返回轴点的秩
}

DUP版本的特点

1. 基本性能
   • 可以正确地处理一般情况
   • 复杂度并未实质增高
2. 对相等元素的处理
   • 遇到连续的相等元素时：
     • lo和hi会交替移动
     • 切分点接近于(lo+hi)/2
3. 算法特性变化
   • 从LUG版的”勤于拓展、懒于交换”
   • 转变为”懒于拓展、勤于交换”
   • 交换操作数量增加
   • 排序稳定性进一步降低

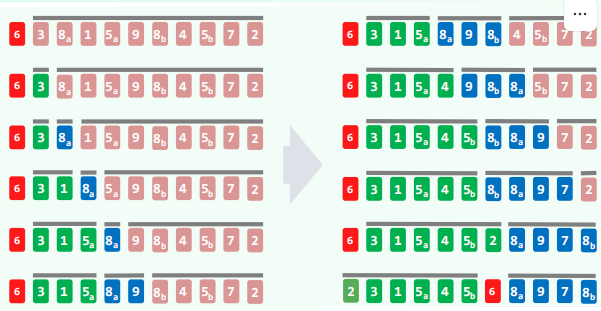
快速划分：LGU版

• 不变性：S=[lo,hi)=[lo]+(lo,mi]+(mi,k)+[k,hi)=pivot+L+G+U

• 单调性：

  • 如果 [k] 不小于轴点：直接扩展 G 区域
  • 否则：G 区域滚动后移，扩展 L 区域

template <typename T> // 轴点构造算法：通过调整元素位置构造区间[lo, hi)的轴点，并返回其秩
Rank Vector<T>::partition(Rank lo, Rank hi)
{                                                    // LGU版
    swap(_elem[lo], _elem[lo + rand() % (hi - lo)]); // 任选一个元素与首元素交换
    T pivot = _elem[lo];                             // 以首元素为候选轴点——经以上交换，等效于随机选取
    Rank mi = lo;

    for (Rank k = lo + 1; k < hi; k++)   // 自左向右扫描
        if (_elem[k] < pivot)            // 若当前元素_elem[k]小于pivot，则
            swap(_elem[++mi], _elem[k]); // 将_elem[k]交换至原mi之后，使L子序列向右扩展

    swap(_elem[lo], _elem[mi]); // 候选轴点归位
    return mi;                  //[lo,mi) < [mi] <= (mi,hi)
}

实例