Sorting - Selection

选取：众数

K-Selection

在任意一组可比较大小的元素中，如何由小到大，找到次序为k者？ 亦即，在这组元素的非降排序序列S中，找出S[k]。

Median (中位数)

• 长度为n的有序序列S中，元素S[n/2]称作中位数（与之相等者也是）
• 在任意一组可比较大小的元素中，如何找到中位数？（Excel：median(range)）

中位数是k-选取的一个特例；稍后将看到，也是其中难度最大者

Majority (众数)

定义

无序向量中，若有一半以上元素同为m，则称之为众数

示例

• 在[3, 5, 2, 3, 3]中众数为3
• 在[3, 5, 2, 3, 3, 0]中，无众数

算法思路

1. 平凡算法 = 排序 + 扫描
   • 限制条件：时间不超过O(n)，附加空间不超过O(1)
   • 必要性：众数若存在，则亦必是中位数

template <typename T> bool majority(Vector<T> A, T & maj) {
    return majCheck(A, maj = median(A));
}

必要条件

在高效的中位数算法未知之前，如何确定众数的候选呢？

mode：众数若存在，则亦必是频繁数（Excel：mode(range)）

template <typename T> bool majority(Vector<T> A, T & maj) {
    return majCheck(A, maj = mode(A));
}

mode()算法难以兼顾时间、空间的高效

可行思路：借助功能更弱但计算成本更低的必要条件，选出唯一的候选者

template <typename T> bool majority(Vector<T> A, T & maj) {
    return majCheck(A, maj = majCandidate(A));
}

减而治之

• 若在向量A的前缀P（ $ \vert P \vert $ 为偶数）中，元素x出现的次数恰占半数，则A有众数，仅当对应的后缀A−P有众数m，且m就是A的众数
• 既然最终总要花费O(n)时间做验证，故而只需考虑A的确含有众数的两种情况：
  1. 若x = m，则在排除前缀P之后，m与其它元素在数量上的差距保持不变
  2. 若x ≠ m，则在排除前缀P之后，m与其它元素在数量上的差距不致缩小

思考：若将众数的标准从”一半以上”改作”至少一半”，算法需做什么调整？

template <typename T> T majCandidate( Vector<T> A ) { //选出具备必要条件的众数候选者
   T maj; //众数候选者
// 线性扫描：借助计数器c，记录maj与其它元素的数量差额
   for ( Rank c = 0, i = 0; i < A.size(); i++ )
      if ( 0 == c ) { //每当c归零，都意味着此时的前缀P可以剪除
         maj = A[i]; c = 1; //众数候选者改为新的当前元素
      } else //否则
         maj == A[i] ? c++ : c--; //相应地更新差额计数器
   return maj; //至此，原向量的众数若存在，则只能是maj —— 尽管反之不然
}  

选取：中位数

归并向量的中位数

给定两个有序向量 $ S_1 $ 和 $ S_2 $ ，长度分别为 $ n_1 $ 和 $ n_2 $ ，如何快速找出 $ S = S_1 \cup S_2 $ 的中位数？

蛮力算法

• 经归并得到有序向量 $ S $
• 取 $ S[(n_1+n_2)/2] $ 即是
• 时间复杂度： $ O(n_1+n_2) $

虽然可行，但未能充分利用 $ S_1 $ 和 $ S_2 $ 的有序性。以下先解决 $ n_1=n_2 $ 的情况，采用减而治之策略。

等长子向量：构思

考查：

• $ m_1 = S_1[\lfloor n/2 \rfloor] $
• $ m_2 = S_2[\lceil n/2 \rceil-1] = S_2[\lfloor(n-1)/2\rfloor] $

可能出现三种情况：

1. 若 $ m_1 = m_2 $ ，则它们同为 $ S_1 $ 、 $ S_2 $ 和 $ S $ 的中位数

2. 若 $ m_1 < m_2 $ ，则 $ n $ 无论偶奇，必有：

   $ median(S_1 \cup S_2) = median(S_1.suffix(\lceil n/2 \rceil) \cup S_2.prefix(\lceil n/2 \rceil)) $

   这意味着，如此减除（一半规模）之后，中位数不变

3. 若 $ m_1 > m_2 $ 时同理

等长子向量：实现

template <typename T> // S1[lo1, lo1 + n)和S2[lo2, lo2 + n)分别有序，n > 0，数据项可能重复
T median( Vector<T>& S1, Rank lo1, Vector<T>& S2, Rank lo2, Rank n ) { //中位数算法（高效版）
   if ( n < 3 ) return trivialMedian( S1, lo1, n, S2, lo2, n ); //递归基
   Rank mi1 = lo1 + n / 2, mi2 = lo2 + ( n - 1 ) / 2; //长度（接近）减半
   if ( S1[mi1] < S2[mi2] )
      return median ( S1, mi1, S2, lo2, n + lo1 - mi1 ); //取S1右半、S2左半
   else if ( S1[mi1] > S2[mi2] )
      return median ( S1, lo1, S2, mi2, n + lo2 - mi2 ); //取S1左半、S2右半
   else
      return S1[mi1];
}

任意子向量：实现

template <typename T> //向量S1[lo1, lo1 + n1)和S2[lo2, lo2 + n2)分别有序，数据项可能重复
T median ( Vector<T>& S1, Rank lo1, Rank n1, Vector<T>& S2, Rank lo2, Rank n2 ) { //中位数算法
   if ( n1 > n2 ) return median( S2, lo2, n2, S1, lo1, n1 ); //确保n1 <= n2
   if ( n2 < 6 ) //递归基：1 <= n1 <= n2 <= 5
      return trivialMedian( S1, lo1, n1, S2, lo2, n2 );

   if ( 2 * n1 < n2 ) //若两个向量的长度相差悬殊，则长者（S2）的两翼可直接截除
      return median( S1, lo1, n1, S2, lo2 + ( n2 - n1 - 1 ) / 2, n1 + 2 - ( n2 - n1 ) % 2 );

   Rank mi1 = lo1 + n1 / 2;
   Rank mi2a = lo2 + ( n1 - 1 ) / 2;
   Rank mi2b = lo2 + n2 - 1 - n1 / 2;
   if ( S1[mi1] > S2[mi2b] ) //取S1左半、S2右半
      return median( S1, lo1, n1 / 2 + 1, S2, mi2a, n2 - ( n1 - 1 ) / 2 );
   else if ( S1[mi1] < S2[mi2a] ) //取S1右半、S2左半
      return median( S1, mi1, ( n1 + 1 ) / 2, S2, lo2, n2 - n1 / 2 );
   else //S1保留，S2左右同时缩短
      return median( S1, lo1, n1, S2, mi2a, n2 - ( n1 - 1 ) / 2 * 2 );
} //O( log(min(n1,n2)) )——可见，实际上等长版本才是难度最大的

选取：QuickSelect

1. 蛮力法

对A排序                     // O(nlogn)
从首元素开始，向后行进k步    // O(k) = O(n)

2. 堆方法 A

将所有元素组织为小顶堆      // O(n)
连续调用k+1次delMin()     // O(klogn)

3. 堆方法 B

L = heapify(A[0, k])     // 任选k+1个元素，组织为大顶堆：O(k)
for each i in (k, n)     // O(n - k)
    L.insert(A[i])       // O(logk)
    L.delMax()           // O(logk)
return L.getMax()

4. 堆方法 C

// 初始化
将输入任意划分为规模为k、n-k的子集
分别组织为大、小顶堆        // O(k + (n-k)) = O(n)

// 主循环
while (M > m)            // O(min(k, n-k))
    swap(M, m)
    L.percolateDown()    // O(logk)
    G.percolateDown()    // O(log(n-k))
return m = G.getMin()

算法下界与最优性分析

问：是否存在更快的算法？

• 显然，最快也不可能快过 O(n)
• 因为第k小是相对于序列整体而言
• 在访问每个元素至少一次之前，无法确定结果

问：是否存在 O(n) 的算法？

template <typename T> Rank quickSelect( T const * A, Rank n, Rank k ) { //基于快速划分的k选取算法
   Vector<Rank> R(n); for ( Rank i = 0; i < n; i++ ) R.insert(i); //使用索引向量，保持原序列的次序
   for ( Rank lo = 0, hi = n; ; ) { //反复做quickParititon
      swap( R[lo], R[lo + rand()%(hi-lo)] ); T pivot = A[R[lo]]; Rank mi = lo; //大胆猜测
      for ( Rank i = lo+1; i < hi; i++ ) //LGU版partition算法
         if ( A[R[i]] < pivot )
            swap( R[++mi], R[i] );
      swap( R[lo], R[mi] ); //[0,mi) < [mi] <= (mi, n)
      if ( mi < k ) lo = mi + 1; //猜小了，则剪除前缀
      else if ( k < mi ) hi = mi; //猜大了，则剪除后缀
      else return R[mi]; //或早或迟，总能猜中
   }
}

期望性能

对于所有情况，记期望的比较次数为 $ T(n) $ ，于是：

$ T(1)=0, T(2)=1, \ldots $

\[\begin{aligned} T(n) &= (n-1)+\frac{1}{n} \times \sum_{k=0}^{n-1} \max \{T(k), T(n-k-1)\} \\ &= (n-1)+\frac{1}{n} \times \sum_{k=0}^{n-1} T(\max \{k, n-k-1\}) \\ &\leq (n-1)+\frac{2}{n} \times \sum_{k=n/2}^{n-1} T(k) \end{aligned}\]

事实上，不难验证： $ T(n) < 4 \cdot n = \mathcal{O}(n) $

\[T(n) \leq (n-1)+\frac{2}{n} \times \sum_{k=n/2}^{n-1} 4k \leq (n-1)+3n < 4n\]

选取：LinearSelect

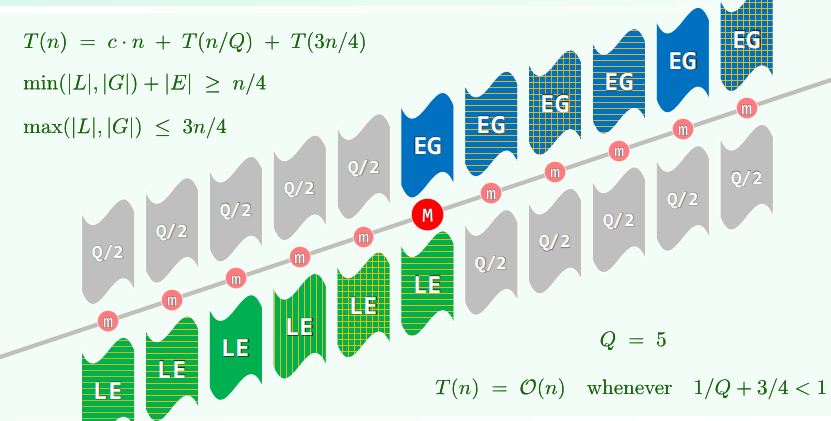
linearSelect(A, n, k)

设 Q 为一个较小的常数：

1. if (n = $ \vert A \vert $ < Q) return trivialSelect(A, n, k)
2. else 将 A 平均分为 n/Q 个子序列（每个大小为 Q）
3. 对每个子序列排序并确定 n/Q 个中位数 // 例如使用插入排序
4. 递归调用 linearSelect() 找到 M，即中位数的中位数

5. 令 L/E/G = { x </=/> M

   x ∈ A }

6. if (k < $ \vert L \vert $ ) return linearSelect(A, $ \vert L \vert $ , k) if (k < $ \vert L \vert $ + $ \vert E \vert $ ) return M return linearSelect(A+ $ \vert L \vert $ + $ \vert E \vert $ , $ \vert G \vert $ , k- $ \vert L \vert $ - $ \vert E \vert $ )

复杂度

将 linearSelect() 算法的运行时间记作 T(n)：

• 第1步：O(1) = O(QlogQ) // 递归基：序列长度 $ \vert A \vert $ ≤ Q
• 第2步：O(n) // 子序列划分
• 第3步：O(n) = Q² × n/Q // 子序列各自排序，并找到中位数
• 第4步：T(n/Q) // 从n/Q个中位数中，递归地找到全局中位数
• 第5步：O(n) // 划分子集L/E/G，并分别计数 —— 一趟扫描足矣
• 第6步：T(3n/4) // 为什么…