Sorting - Shell Sort

框架 + 实例

D. L. Shell 的基本思想：将整个序列视作一个矩阵，逐列各自排序

递减增量（diminishing increment）算法特点：

• 由粗到细：重排矩阵，使其更窄，再次逐列排序（h-sorting/h-sorted）
• 逐步求精：如此往复，直至矩阵变成一列（1-sorting/1-sorted）

关键概念：

• 步长序列（step sequence）：由各矩阵宽度逆向排列而成的序列
• 正确性：最后一次迭代等同于全排序（1-sorted = ordered）
• 实现方式：Call-by-rank

实现细节

矩阵重排的实现：

• 无需使用二维向量
• 一维向量即可完成操作
• 在矩阵宽度为 h 时的映射关系：
  • B[i][j] = A[i·h + j]
  • A[k] = B[⌊k/h⌋][k mod h]

template <typename T> //向量希尔排序
void Vector<T>::shellSort( Rank lo, Rank hi ) { // 0 <= lo < hi <= size <= 2^31
   for ( Rank d = 0x7FFFFFFF; 0 < d; d >>= 1 ) // PS Sequence: { 1, 3, 7, 15, 31, ... }
      for ( Rank j = lo + d; j < hi; j++ ) { // for each j in [lo+d, hi)
         T x = _elem[j]; Rank i = j; // within the prefix of the subsequence of [j]
         while ( ( lo + d <= i ) && ( x < _elem[i - d] ) ) // find the appropriate
            _elem[i] = _elem[i - d], i -= d; // predecessor [i]
         _elem[i] = x; // where to insert [j]
      }
}

Shell序列 + 输入敏感性

Shell序列的最坏情况分析

实际上，采用 $ H_{shell} $ 序列在最坏情况下需要运行 $ \Omega(N^2) $ 时间：

• 考虑由子序列 $ A = unsort[0, 2^{N-1}) $ 和 $ B = unsort[2^{N-1}, 2^N) $ 交错而成的序列
• 在进行 2-sorting 时，A、B 各自成一列，此后必然各自有序
• 然而其中的逆序对依然很多，最后的 1-sorting 仍需 $ \Omega(n^2/4) $ 时间
• 问题的根源在于， $ H_{shell} $ 中各项并不互素，甚至相邻项也非互素

Postage Problem（邮资问题）

问题描述：

• 信件邮资为 50F
• 明信片邮资为 35F
• 仅有面值为 4F 和 13F 的邮票
• 问：能否用现有邮票精确支付信件和明信片的邮资？

形式化表述： 给定邮资 P，判断是否 $ P \in { n\cdot4 + m\cdot13 \mid n,m \in \mathbb{N} } $

线性组合（Linear Combination）

• 设 $ g,h \in \mathcal{N} $
• 对任意 $ n,m \in \mathcal{N} $ ， $ n\cdot g + m\cdot h $ 称为 g 和 h 的线性组合

定义：

\[\begin{array}{l} \mathbf{C}(g,h) = \{ng + mh \mid n,m \in \mathcal{N}\} \\ \mathbf{N}(g,h) = \mathcal{N} \setminus \mathbf{C}(g,h) \quad \text{// 不能表示为g和h线性组合的数} \\ \mathbf{x}(g,h) = \max\{\mathbf{N}(g,h)\} \quad \text{// 是否一定存在？} \end{array}\]

定理：当 g 和 h 互素时，有：

\[\begin{aligned} \mathbf{x}(g,h) &= (g-1)\cdot(h-1)-1 = gh-g-h \\ \text{例如：}\quad \mathbf{x}(3,7) &= 11,\quad \mathbf{x}(4,9)=23,\quad \mathbf{x}(4,13)=35,\quad \mathbf{x}(5,14)=51 \end{aligned}\]

h-sorting 与 h-ordered

h-ordered 定义：

• 对序列 $ S[0,n) $ ，若对所有 $ i \in [0, n-h) $ 都有 $ S[i] \leq S[i+h] $ ，则称该序列为 h-ordered
• 特别地，1-ordered 序列即为有序序列

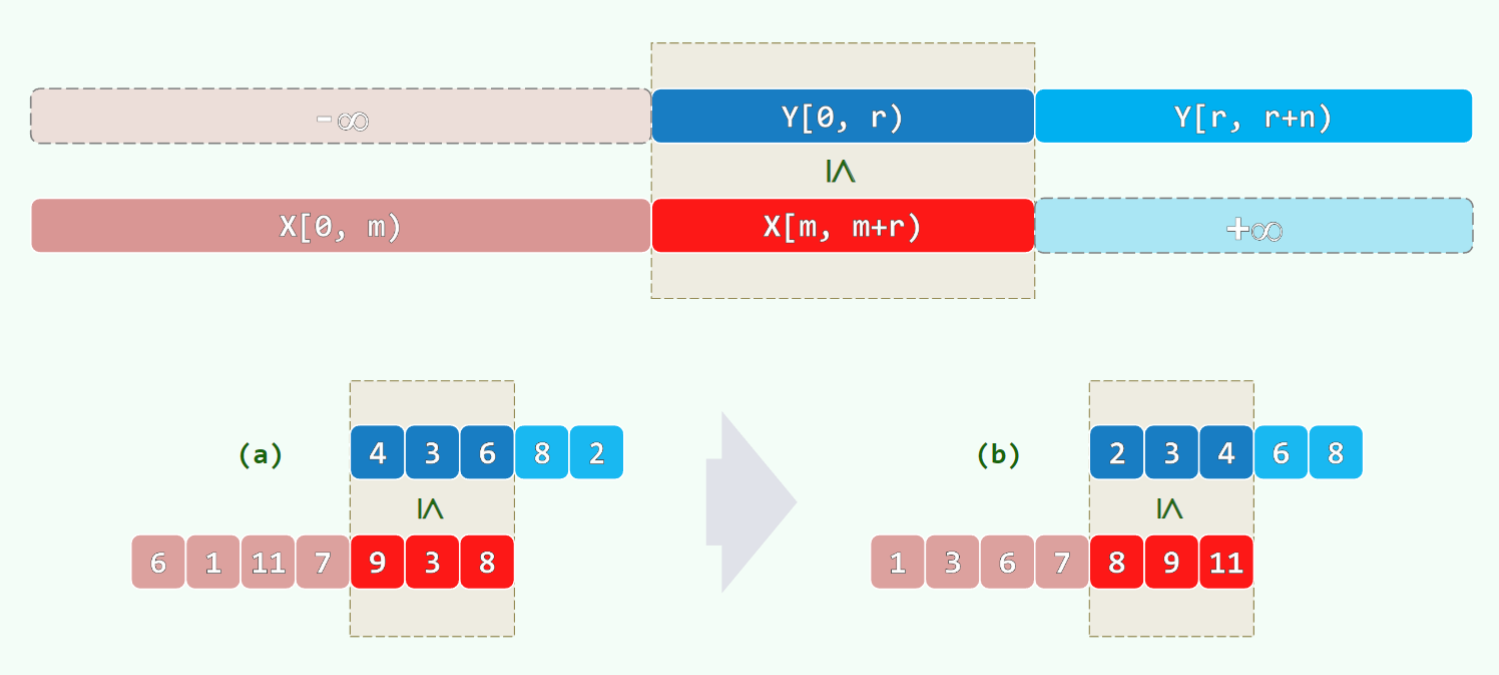
h-sorting 过程： 通过以下步骤获得 h-ordered 序列：

1. 将序列 S 重排为具有 h 列的二维矩阵
2. 对每一列分别进行排序

定理 K

若序列为 g-ordered，则在经过 h-sorting 后仍然保持 g-ordered。

引理 L

线性组合性质

若一个序列同时是 g-ordered 和 h-ordered，则称为 (g,h)-ordered，此时该序列：

• 必然是 $ (g+h) $ -ordered
• 对任意 $ m,n \in \mathbb{N} $ ，必然是 $ (mg+nh) $ -ordered

逆序性质

设序列 $ S[0,n) $ 为 $ (g,h) $ -ordered，其中 g 和 h 互素，则：

对于序列中的任意元素 $ S[j] $ 和 $ S[i] $ ，有：

$ i - j > x(g,h) $ 时必有 $ S[j] \leq S[i] $

这表明：

• 对于每个元素，在其左侧只有前 $ x(g,h) $ 个元素可能大于它
• 整个序列中的逆序对数量不超过 $ n \cdot x(g,h) $

PS 序列

如果 $ g $ 和 h 互素且都是 $ \mathcal{O}(d) $ 的，我们可以在 $ \mathcal{O}(dn) $ 时间内完成 d-sorting：

• 将序列重排为具有 d 列的二维矩阵
• 每个元素最多与 $ \mathcal{O}((g-1)(h-1)/d) = \mathcal{O}(d) $ 个元素交换

由于这对所有元素都成立，因此总共需要 $ \mathcal{O}(dn) $ 步骤

Papernov-Stasevic 序列（又称 Hibbard 序列）

\[\mathcal{H}_{PS} = \mathcal{H}_{\text{Shell}}-1 = \{2^k-1 \mid k \in \mathcal{N}\} = \{1,3,7,15,31,63,127,255,\ldots\}\]

• 不同项可能不互素，例如 $ h_{2k} = h_k\cdot(h_k+2) $
• 但相邻项必然互素，因为 $ h_{k+1}-2\cdot h_k \equiv 1 $
• 使用 $ \mathcal{H}_{PS} $ 的 Shellsort 需要：
  • $ \mathcal{O}(\log n) $ 次外部迭代
  • $ \mathcal{O}(n^{3/2}) $ 时间来排序长度为 n 的序列

时间复杂度分析

令 $ h_t $ 为最接近 $ \sqrt{n} $ 的步长值，因此 $ h_t \approx \sqrt{n}=\Theta(n^{1/2}) $

1. 当 t < k 时的迭代分析

考虑迭代序列 $ {h_k \mid t < k} = {\overleftarrow{h_{t+1}, h_{t+2}, …, h_m}} $

• 因为每个 $ h_k $ 列中有 $ \mathcal{O}(n/h_k) $ 个元素
• 所以对每列进行插入排序需要 $ \mathcal{O}((n/h_k)^2) $ 时间
• 因此每次 $ h_k $ -sorting 需要 $ \mathcal{O}(n^2/h_k) $ 时间

综上所述，这些迭代的总时间复杂度为： $ \mathcal{O}(2 \times n^2/h_t) = \mathcal{O}(n^{3/2}) $

2. 当 k ≤ t 时的迭代分析

考虑迭代序列 $ {h_k \mid k \leq t} = {\overleftarrow{h_1, h_2, …, h_t}} $

• 因为 $ h_{k+1} $ 和 $ h_{k+2} $ 互素且都是 $ \mathcal{O}(h_k) $ 量级
• 所以每次 $ h_k $ -sorting 需要 $ \mathcal{O}(n \times h_k) $ 时间
• 因此这些迭代的总时间复杂度为 $ \mathcal{O}(n \times 2 \cdot h_t) = \mathcal{O}(n^{3/2}) $

注意：

• 这个上界是紧确的
• 平均情况下，根据模拟实验为 $ \mathcal{O}(n^{5/4}) $ ，但尚未被证明

Pratt 序列

Pratt 序列（1971）定义如下：

\[\begin{aligned} \mathcal{H}_{\text{pratt}} &= \{2^p \cdot 3^q \mid p,q \in \mathcal{N}\} \\ &= \{1,2,3,4,6,8,9,12,16,18,24,27,32,36,\ldots\} \end{aligned}\]

重要特性：

• 相邻项不一定互素
• 不大于 n 的项数为 $ \mathcal{O}(\log^2 n) $
• 使用 Pratt 序列的 Shellsort 可以在 $ \mathcal{O}(n\log^2 n) $ 时间内完成排序

从 (2,3)-ordered 到 1-ordered

由于 $ \mathbf{x}(2,3) = 2 \cdot 3 - 2 - 3 = 1 $ ，可知：

• 在 (2,3)-ordered 序列中，每个元素左侧只有相邻元素可能比它小
• 因此排序这样的序列只需 $ \mathcal{O}(n) $ 时间

从 $ (2h_k, 3h_k) $ -ordered 到 $ h_k $ -ordered

排序过程：

1. 将序列 S 分解为 $ h_k $ 个子序列，每个子序列都是 (2,3)-ordered
2. 分别对这些子序列进行排序，总共需要 $ \mathcal{O}(n) $ 时间
3. 由于总共有 $ \mathcal{O}(\log^2 n) $ 次迭代
4. 因此总时间复杂度为 $ \mathcal{O}(n\log^2 n) $

Sedgewick 序列

背景：

• Pratt 序列需要太多迭代次数，对预排序序列效果不佳
• Sedgewick 序列结合了 PS 序列和 Pratt 序列的优点

定义：

\[\{9 \cdot 4^k - 9 \cdot 2^k + 1 \mid k \geq 0\} \cup \{4^k - 3 \cdot 2^k + 1 \mid k \geq 2\}\]

性能：

• 最坏情况： $ \mathcal{O}(n^{4/3}) $
• 平均情况： $ \mathcal{O}(n^{7/6}) $
• 实践中表现最佳

开放问题： 是否存在最坏情况下时间复杂度为 $ \mathcal{O}(n\log n) $ 的步长序列？