String - BM Algorithm

写在前面

在计算机科学里，Boyer-Moore字符串搜索算法是一种非常高效的字符串搜索算法。它由Bob Boyer和J Strother Moore设计于1977年。此算法仅对搜索目标字符串（关键字）进行预处理，而非被搜索的字符串。虽然Boyer-Moore算法的执行时间同样线性依赖于被搜索字符串的大小，但是通常仅为其它算法的一小部分：它不需要对被搜索的字符串中的字符进行逐一比较，而会跳过其中某些部分。通常搜索关键字越长，算法速度越快。它的效率来自于这样的事实：对于每一次失败的匹配尝试，算法都能够使用这些信息来排除尽可能多的无法匹配的位置。

在学习研究BM算法之前，最好已经掌握KMP算法，所以建议还没有掌握的同学，先去学习一下，循序渐进的来，可以看KMP算法。为什么说循序渐进，是因为BM算法在大多数情况下表现的比KMP算法优秀，所以大部分时候，都当做KMP进阶的算法来学习。BM算法从模式串的尾部开始匹配，且拥有在最坏情况下 O(N) 的时间复杂度。有数据表明，在实践中，比 KMP 算法的实际效能高，可以快大概 3-5 倍，很值得学习。

BM 算法原理

BM算法定义了两个规则：

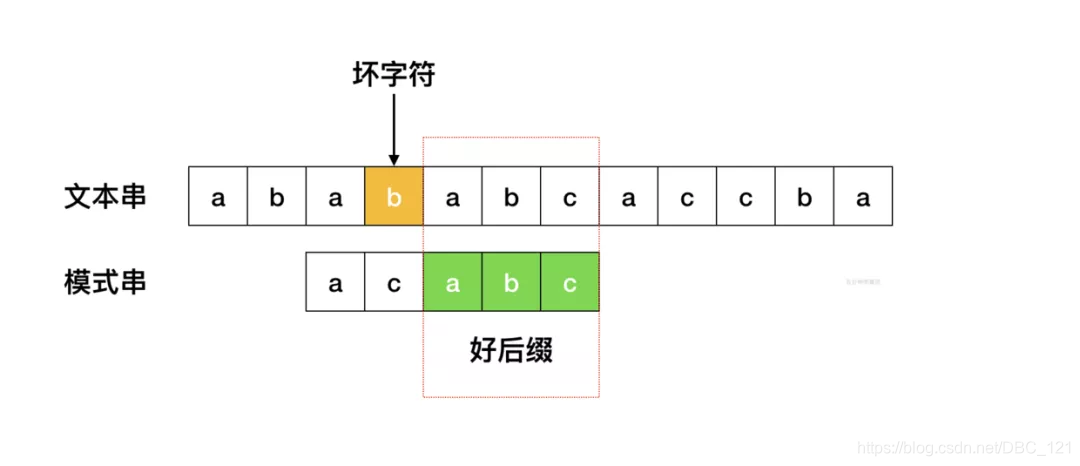
• 坏字符规则： 当文本串中的某个字符跟模式串的某个字符不匹配时，我们称文本串中的这个失配字符为坏字符，此时模式串需要向右移动，移动的位数 = 坏字符在模式串中的位置 - 坏字符在模式串中最右出现的位置。此外，如果”坏字符”不包含在模式串之中，则最右出现位置为-1。
• 好后缀规则： 当字符失配时，后移位数 = 好后缀在模式串中的位置 - 好后缀在模式串上一次出现的位置，且如果好后缀在模式串中没有再次出现，则为-1。

下面举例说明BM算法。例如，给定文本串”HERE IS A SIMPLE EXAMPLE“，和模式串”EXAMPLE“，现要查找模式串是否在文本串中，如果存在，返回模式串在文本串中的位置。

• 首先，”文本串”与”模式串”头部对齐，从尾部开始比较。”S“与”E“不匹配。这时，”S“就被称为”坏字符”（bad character），即不匹配的字符，它对应着模式串的第6位。且”S“不包含在模式串”EXAMPLE“之中（相当于最右出现位置是-1），这意味着可以把模式串后移6-(-1)=7位，从而直接移到”S“的后一位。

    HERE IS A SIMPLE EXAMPLE
          |
    EXAMPLE
  

• 依然从尾部开始比较，发现”P“与”E“不匹配，所以”P“是”坏字符”。但是，”P“包含在模式串”EXAMPLE“之中。因为”P“这个”坏字符”对应着模式串的第6位（从0开始编号），且在模式串中的最右出现位置为4，所以，将模式串后移6-4=2位，两个”P“对齐。

    HERE IS A SIMPLE EXAMPLE
                 |
           EXAMPLE
  
    HERE IS A SIMPLE EXAMPLE
                 |
             EXAMPLE
  

• 依次比较，得到 “MPLE“匹配，称为”好后缀”（good suffix），即所有尾部匹配的字符串。注意，”MPLE“、”PLE“、”LE“、”E“都是好后缀。

    HERE IS A SIMPLE EXAMPLE
                ||||
             EXAMPLE
  

• 发现”I“与”A“不匹配：”I“是坏字符。如果是根据坏字符规则，此时模式串应该后移2-(-1)=3位。问题是，有没有更优的移法？

    HERE IS A SIMPLE EXAMPLE
               |
             EXAMPLE
  
    HERE IS A SIMPLE EXAMPLE
                |
                EXAMPLE
  

• 更优的移法是利用好后缀规则：当字符失配时，后移位数 = 好后缀在模式串中的位置 - 好后缀在模式串中上一次出现的位置，且如果好后缀在模式串中没有再次出现，则为-1。所有的”好后缀”（MPLE、PLE、LE、E）之中，只有”E“在”EXAMPLE“的头部出现，所以后移6-0=6位。可以看出，”坏字符规则”只能移3位，”好后缀规则”可以移6位。每次后移这两个规则之中的较大值。这两个规则的移动位数，只与模式串有关，与原文本串无关。

    HERE IS A SIMPLE EXAMPLE
                         |
                   EXAMPLE
  

• 继续从尾部开始比较，”P“与”E“不匹配，因此”P“是”坏字符”，根据”坏字符规则”，后移 6 - 4 = 2 位。因为是最后一位就失配，尚未获得好后缀。

    HERE IS A SIMPLE EXAMPLE
                           |
                     EXAMPLE
  

好后缀加深理解

由上可知，BM算法不仅效率高，而且构思巧妙，容易理解。坏字符规则相对而言比较好理解，好后缀如果还不理解，我这里再继续举个例子解释一下，这里加深理解。

如果字符串”ABCDAB“的后一个”AB“是”好后缀”。那么它的位置是5（从0开始计算，取最后的”B“的值），在”搜索词中的上一次出现位置”是1（第一个”B“的位置），所以后移 5 - 1 = 4 位，前一个”AB“移到后一个”AB”的位置。

再举一个例子，如果字符串”ABCDEF“的”EF“是好后缀，则”EF“的位置是5 ，上一次出现的位置是 -1（即未出现），所以后移 5 - (-1) = 6 位，即整个字符串移到”F“的后一位。

这个规则有三个注意点：

1. “好后缀”的位置以最后一个字符为准。假定”ABCDEF“的”EF“是好后缀，则它的位置以”F“为准，即5（从0开始计算）。

2. 如果”好后缀”在搜索词中只出现一次，则它的上一次出现位置为 -1。比如，”EF“在”ABCDEF“之中只出现一次，则它的上一次出现位置为-1（即未出现）。

3. 如果”好后缀”有多个，则除了最长的那个”好后缀”，其他”好后缀”的上一次出现位置必须在头部。比如，假定”BABCDAB“的”好后缀”是”DAB“、”AB“、”B“，请问这时”好后缀”的上一次出现位置是什么？回答是，此时采用的好后缀是”B“，它的上一次出现位置是头部，即第0位。这个规则也可以这样表达：如果最长的那个”好后缀”只出现一次，则可以把搜索词改写成如下形式进行位置计算”(DA)BABCDAB“，即虚拟加入最前面的”DA“。

这一规律与技巧与 KMP 如出一辙，只不过前后颠倒而已。回到上文的这个例子。此时，所有的”好后缀”（MPLE、PLE、LE、E）之中，只有E在EXAMPLE还出现在头部，所以后移 6 - 0 = 6 位。

代码实现

int match( char* P, char* T ) { //Boyer-Morre算法（简化版，只考虑Bad Character Shift）
   int* bc = buildBC( P ); //预处理
   int n = strlen( T ), i; //文本串长度、与模式串首字符的对齐位置
   int m = strlen( P ), j; //模式串长度、模式串当前字符位置
   for ( i = 0; i+m <= n; i += max(1, j - bc[ T[i+j] ]) ) { //不断右移P
      for ( j = m-1; (0 <= j) && (P[j] == T[i+j]); j-- ); //自右向左逐个比对
      if ( j < 0 ) break; //一旦完全匹配，随即收工
   }
   delete [] bc; return i; //销毁BC表，返回最终的对齐位置
}

int* buildBC( char* P ) { //构造Bad Charactor Shift表：O(m + 256)
int* bc = new int[256]; // BC表，与字符表等长
for ( size_t j = 0; j < 256; j++ ) bc[j] = -1; //初始化：首先假设所有字符均未在P中出现
for ( size_t m = strlen( P ), j = 0; j < m; j++ ) //自左向右扫描模式串P
    bc[P[j]] = j; //将字符P[j]的BC项更新为j（单调递增）——画家算法
return bc;
}

性能分析

BM算法的高效性体现在其空间和时间复杂度的平衡，以及在实践中的优异性能。

空间复杂度

BM算法在构造过程中需要使用坏字符表（bc）和好后缀表（gs）来进行预处理，这两个表的空间复杂度为：

• 坏字符表（bc）： 需要存储与字符集大小 |Σ| 等长的数组。常见字符集（如ASCII或Unicode）大小固定，因此通常可以认为是常量。
• 好后缀表（gs）： 需要存储模式串长度 m 等长的数组。

因此，BM算法的总体空间复杂度为： 空间复杂度 = O(|Σ| + m)

时间复杂度

BM算法的时间复杂度取决于模式串的预处理时间和查找过程中对文本串的操作时间。

1. 预处理时间：
   • 构造坏字符表的时间复杂度为 O(|Σ| + m)，因为需要遍历字符集并扫描模式串。
   • 构造好后缀表的时间复杂度为 O(m)，因为仅需对模式串进行一次从右向左的扫描。
   • 总预处理时间：O(|Σ| + m)
2. 查找效率：
   • 最好情况： 当每次移动都跳过整个模式串长度（即O(m)），查找操作的复杂度为 O(n / m)，其中 n 是文本串长度，m 是模式串长度。
     最好情况发生在坏字符规则和好后缀规则都能实现最大跳跃时。
     查找时间复杂度：O(n / m)
   • 最坏情况： 模式串在文本串中每次只移动一位，此时总比对次数为 O(n + m)。
     查找时间复杂度：O(n + m)

性能关键因素

BM算法的实际性能取决于以下关键因素：

1. 单次比对成功的概率（Pr）：
   单次比对成功的概率直接影响算法的跳跃距离和整体效率。通常，比对成功的概率可以用 1 / |Σ| 来估计，其中 |Σ| 是字符集的大小。例如，对于ASCII字符集，|Σ| = 256，因此 Pr ≈ 1/256。

2. 模式串的长度（m）：
   模式串越长，BM算法的跳跃距离越大，因此性能提升越明显。长模式串更容易利用坏字符规则和好后缀规则的跳跃特性，从而减少对文本串的扫描次数。

3. 字符分布的随机性：
   如果文本串和模式串的字符分布不均匀（即某些字符出现频率较高），则坏字符规则可能会受到限制，从而影响跳跃效率。均匀分布的字符更有利于BM算法的性能。